Question 147138: 2. In a certain triangle the measure of one angle is double the measure of a second angle but is 5 degrees less than the measure of the third angle. If the sum of the measures of the three interior angles of a triangle is always 180 degrees, form an algebraic equation to express the problem, and identify the variables, coefficients, and constants of the algebraic expression.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2. In a certain triangle the measure of one angle is double the measure of a second angle but is 5 degrees less than the measure of the third angle. If the sum of the measures of the three interior angles of a triangle is always 180 degrees, form an algebraic equation to express the problem, and identify the variables, coefficients, and constants of the algebraic expression.
:
Let x = "second angle"
then
2x = "one angle"
and it says:
"One angle.....is 5 degrees less than the measure of the third angle." we can say:
2x + 5 = "third angle"
:
1st angle + 2nd angle + 3rd angle = 180 degree
2x + x + (2x+5) = 180
:
5x + 5 = 180
5x = 180 - 5
5x = 175
x = 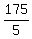
x = 35 degrees is the 2nd angle
then
70 degrees is the 1st angle
and
75 degrees is the 3rd angle
:
Using the equation: 5x = 175
The variable is x, the coefficient is 5, and 175 is the constant
|
|
|