Question 146997: I need help dividing this problem
x^2 – 3x + 2 ÷ x^2 – 1
7x – 14 7x + 7
I can not figure out how to write the number as it appears on paper
x^2-3x+2 are underlined and so is x^2-1 ( didn't know if that made a difference)
Answer by mangopeeler07(462)   (Show Source): (Show Source):
You can put this solution on YOUR website! As a shortcut: Just put the first numerator over the second and the first denominator over the second. you should get 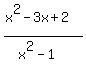 and and 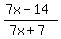 . Then factor every expression. After this you should end up with . Then factor every expression. After this you should end up with  and and 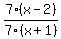 . Then for each fraction, cancel out like things in the numerator and the denominator. You should end up with . Then for each fraction, cancel out like things in the numerator and the denominator. You should end up with 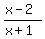 for each of those fractions. Then simply divide them by each other, since that was the original problem (division). Since they are the same thing, their quotient has to be one, because anything divided by itself is one. So your answer is 1. for each of those fractions. Then simply divide them by each other, since that was the original problem (division). Since they are the same thing, their quotient has to be one, because anything divided by itself is one. So your answer is 1.
Doing it the conventional way works too. Just have the fractions as written from the beginning, flip the second one, factor the expressions, and this time when you cancel things out, it will be diagonally and vertically, instead of only vertically as in the shortcut. Your answer will be 1. Try it!
First flip the second fraction and set it up as multiplication (which you did not have to do in the shortcut). Factor and get 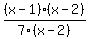 and and 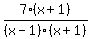 . Once you cancel, you should end up with . Once you cancel, you should end up with  and and 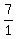 . Multiply them by each other and what do you get? 1! . Multiply them by each other and what do you get? 1!
|
|
|