|
Question 146948: This problem has 3 parts. I figured out the answer to a and b. i only need c.
Let A = (-2,3), B = (6,7), and C = (-1,6).
a.) Find an equation for the perpendicular bisector of AB.
My answer is: y= -3x +3
b.) Find an equation for the perpendicular bisector of BC.
y= -3x + 13
c.) Find coordinates for4 a point K that is equidistant from A, B, and C.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem has 3 parts. I figured out the answer to a and b. i only need c.
Let A = (-2,3), B = (6,7), and C = (-1,6).
a.) Find an equation for the perpendicular bisector of AB.
My answer is: y= -3x +3
Sorry, that's wrong. Plot the two points:
 Find the midpoint using the midpoint formula:
Given the two points (
Find the midpoint using the midpoint formula:
Given the two points ( , ,  ), ( ), ( , ,  ),
Their midpoint = ( ),
Their midpoint = ( , , 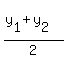 )
Substituting points (-2,3) and (6,7),
Their midpoint = ( )
Substituting points (-2,3) and (6,7),
Their midpoint = ( , , 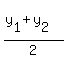 )
= ( )
= (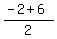 , , 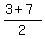 ) = ( ) = ( , ,  ) = ( ) = ( , ,  )
So we plot that, and connect the three points: )
So we plot that, and connect the three points:
 Next we find the slope of AB using the slope formula:
Next we find the slope of AB using the slope formula:
 To find the slope of a line which is perpendicular to
a line with slope
To find the slope of a line which is perpendicular to
a line with slope  , we invert the fraction and
change its sign, and get , we invert the fraction and
change its sign, and get 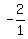 or or  Now since the line goes through (2,5), we use the point-slope
form of a line's equation using
Now since the line goes through (2,5), we use the point-slope
form of a line's equation using  : :
 y-5=-2(x-2)
y-5=-2x+4
y=-2x+9
Now we draw that and get:
y-5=-2(x-2)
y-5=-2x+4
y=-2x+9
Now we draw that and get:
 ---------------------------------
---------------------------------
b.) Find an equation for the perpendicular bisector of BC.
y= -3x + 13
Sorry, that's wrong, too Plot the two points:
 Find the midpoint using the midpoint formula:
Given the two points (
Find the midpoint using the midpoint formula:
Given the two points ( , ,  ), ( ), ( , ,  ),
Their midpoint = ( ),
Their midpoint = ( , , 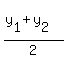 )
Substituting points (6,7) and (-1,6),
Their midpoint = ( )
Substituting points (6,7) and (-1,6),
Their midpoint = ( , , 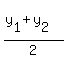 )
= ( )
= (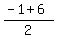 , , 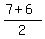 ) = ( ) = ( , , 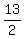 ) = ( ) = ( , ,  )
So we plot that, and connect the three points: )
So we plot that, and connect the three points:
 Next we find the slope of BC using the slope formula:
Next we find the slope of BC using the slope formula:
 To find the slope of a line which is perpendicular to
a line with slope
To find the slope of a line which is perpendicular to
a line with slope  , we invert the fraction and
change its sign, and get , we invert the fraction and
change its sign, and get 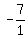 or or  Now since the line goes through (2.5,7.5), we use the point-slope
form of a line's equation using
Now since the line goes through (2.5,7.5), we use the point-slope
form of a line's equation using  : :



 Now we draw that and get:
Now we draw that and get:

c.) Find coordinates for a point K that is equidistant from A, B, and C.
This amounts to finding the center of a circle that passes
through all three points, for the center of a circle is
equidistant from all points on a circle.
AB and BC are both chords. There is a theorem that says,
"The perpendicular bisectors of two chords intersect at the
center of a circle.
 Now we can draw in the circle:
Now we can draw in the circle:
 So we solve the system of the equations of the two perpendicular
bisectors of the above two problems and we get:
So we solve the system of the equations of the two perpendicular
bisectors of the above two problems and we get:

 Solve that system of equations by substitution, which I assume
you can do, and get
x=3, y=3.
So the point (3,3) is the center of the circle, which is
equidistant from all three given points A, B, and C.
Solve that system of equations by substitution, which I assume
you can do, and get
x=3, y=3.
So the point (3,3) is the center of the circle, which is
equidistant from all three given points A, B, and C.
 Edwin
Edwin
|
|
|
| |