SOLUTION: Find the quadratic function that has a vertex at (-1,3) and whose graph passes through the point (2,1).

Algebra ->  Graphs -> SOLUTION: Find the quadratic function that has a vertex at (-1,3) and whose graph passes through the point (2,1).      Log On


   

Question 146893: Find the quadratic function that has a vertex at (-1,3) and whose graph passes through the point (2,1).
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Find the quadratic function that has a vertex at (-1,3) and whose graph passes through the point (2,1).

All quadratic functions are in the form

f%28x%29=a%28x-h%29%5E2+%2B+k

or for convenience, let's write y for f%28x%29

y+=+a%28x-h%29%5E2%2Bk

where the vertex is (h,k).

So since the vertex is (-1,3), we plug those in

y+=+a%28x-h%29%5E2%2Bk

y+=+a%28x-%28-1%29%29%5E2%2B3

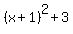y+=+a%28x%2B1%29%5E2%2B3

Now all we need is a

So we substitute (x,y) = (2,1).

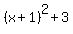y+=+a%28x%2B1%29%5E2%2B3
1+=+a%282%2B1%29%5E2%2B3
1+=+a%283%29%5E2%2B3
1+=+9a%2B3
-2=9a
-2%2F9=a

So

y+=+a%28x%2B1%29%5E2%2B3

becomes

y+=+-2%2F9%28x%2B1%29%5E2%2B3

or

f%28x%29+=+-2%2F9%28x%2B1%29%5E2%2B3

in functional notation.

To draw the graph, plot the given vertex and the given
point, and find some more points, say: 

(-7,-5), (-4,1), (5,-5)



Now draw in the graph of the function:

 
Edwin