Simplify
(5c-3power d4power/p-2power)-1power (p7power d-1power/c2ndpower)2power - simplify and write the answer with all exponents positive.
 We must get rid of the outer exponents. But first we must
make sure every factor inside each parentheses has an
exponent showing. Only the
We must get rid of the outer exponents. But first we must
make sure every factor inside each parentheses has an
exponent showing. Only the  doesn't, so we
write
doesn't, so we
write  as
as 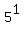
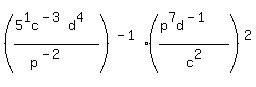 Now we multiply the INNER exponent of every factor, in
both numerator and denominator by the OUTER exponent:
Now we multiply the INNER exponent of every factor, in
both numerator and denominator by the OUTER exponent:
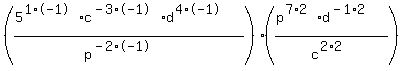 That gets rid of the outer exponents. Now we simplify:
That gets rid of the outer exponents. Now we simplify:
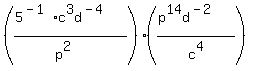 Next, we use these two rules:
1. If a factor with a negative exponent appears as a factor of
the NUMERATOR, then move both base and exponent from the
NUMERATOR to the DENOMINATOR, CHANGING THE SIGN OF THE EXPONENT,
and eliminating base and exponent
from the NUMERATOR.
2. If a factor with a negative exponent appears as a factor of
the DENOMINATOR, then move both base and exponent from the
DENOMINATOR to the NUMERATOR, CHANGING THE SIGN OF THE EXPONENT,
and eliminating base and exponent
from the DENOMINATOR.
Next, we use these two rules:
1. If a factor with a negative exponent appears as a factor of
the NUMERATOR, then move both base and exponent from the
NUMERATOR to the DENOMINATOR, CHANGING THE SIGN OF THE EXPONENT,
and eliminating base and exponent
from the NUMERATOR.
2. If a factor with a negative exponent appears as a factor of
the DENOMINATOR, then move both base and exponent from the
DENOMINATOR to the NUMERATOR, CHANGING THE SIGN OF THE EXPONENT,
and eliminating base and exponent
from the DENOMINATOR.
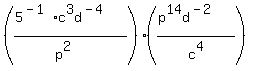 Move the
Move the  from the top to the bottom as
from the top to the bottom as 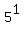
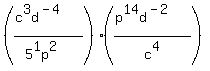 In the left fraction, move the
In the left fraction, move the 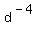 from the top to the
bottom as
from the top to the
bottom as 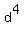
 In the right fraction, move the
In the right fraction, move the 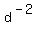 from the top to the
bottom as
from the top to the
bottom as 
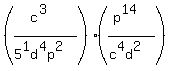 Now let;s indicate the multiplication of the tops
and bottoms and make it all into one fraction:
Now let;s indicate the multiplication of the tops
and bottoms and make it all into one fraction:
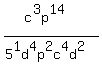 Add the exponents of
Add the exponents of  on the bottom:
on the bottom:
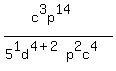
 Now use this rule:
If an exponential with a positive exponent appears as a
factor of the NUMERATOR, and an exponential with the same base
and a positive exponent also appears as a factor of the
DENOMINATOR, then subtract the exponents (LARGER MINUS SMALLER)
and place the base with the resulting exponent in the numerator
or denominator, depending of which one had the larger positive
exponent.
Notice that we have a
Now use this rule:
If an exponential with a positive exponent appears as a
factor of the NUMERATOR, and an exponential with the same base
and a positive exponent also appears as a factor of the
DENOMINATOR, then subtract the exponents (LARGER MINUS SMALLER)
and place the base with the resulting exponent in the numerator
or denominator, depending of which one had the larger positive
exponent.
Notice that we have a 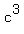 in the top and a
in the top and a 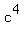 in the
bottom. So we subtract those two exponents (LARGER MINUS SMALLER),
in the
bottom. So we subtract those two exponents (LARGER MINUS SMALLER),
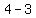 and get
and get  . So we place
. So we place 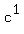 in the BOTTOM because
the larger exponent was in the BOTTOM:
in the BOTTOM because
the larger exponent was in the BOTTOM:
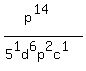 Also notice that we have a
Also notice that we have a 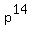 in the top and a
in the top and a  in the
bottom. So we subtract those two exponents (LARGER MINUS SMALLER),
in the
bottom. So we subtract those two exponents (LARGER MINUS SMALLER),
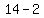 and get
and get  . So we place
. So we place 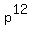 in the TOP because
the larger exponent was in the TOP:
in the TOP because
the larger exponent was in the TOP:
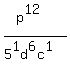 Finally we erase the 1 exponents of 5 and c
Finally we erase the 1 exponents of 5 and c
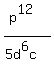 Edwin
Edwin