I need some help with some homework Please!!!!
The directions say: Solve the following polynomial equations using the zero factor property
 Multiply the first number, 3, on the left by the last
number on the left, 2. (Take these as positive).
You get 6. So we write down all the ways to get
two integers that have product 6. These are
products
1 x 6 = 6
2 x 3 = 6
Now look at the sign of the last number in
Multiply the first number, 3, on the left by the last
number on the left, 2. (Take these as positive).
You get 6. So we write down all the ways to get
two integers that have product 6. These are
products
1 x 6 = 6
2 x 3 = 6
Now look at the sign of the last number in
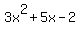 = 0, -2. It is negative, so out beside
the multiplication, subtract the smaller of the
factors from the larger factor:
[Note: if that last sign had been positive, we would add,
not subtract.]
products differences
1 x 6 = 6 6 - 1 = 5
2 x 3 = 6 3 - 2 = 1
= 0, -2. It is negative, so out beside
the multiplication, subtract the smaller of the
factors from the larger factor:
[Note: if that last sign had been positive, we would add,
not subtract.]
products differences
1 x 6 = 6 6 - 1 = 5
2 x 3 = 6 3 - 2 = 1
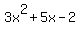 = 0
Since the middle number 5 appears as a difference
between 6 and 1, we use 6 and 1 to rewrite the
middle term "
= 0
Since the middle number 5 appears as a difference
between 6 and 1, we use 6 and 1 to rewrite the
middle term " ".
We rewrite
".
We rewrite  as
as 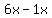 So
So 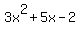 = 0
becomes
= 0
becomes
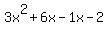 = 0
Now factor 3x out of the first two terms on the left:
= 0
Now factor 3x out of the first two terms on the left:
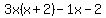 = 0
Now factor -1 out of the last two terms on the left:
= 0
Now factor -1 out of the last two terms on the left:
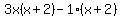 = 0
Now factor out the binomial factor
= 0
Now factor out the binomial factor 
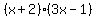 = 0
Set
= 0
Set  which gives solution
which gives solution  Set
Set  which gives solution
which gives solution  --------------------------------------------
--------------------------------------------
 Multiply the first number, 2, on the left by the last
number on the left, 40.
(Take these as positive).
You get 80. So we write down all the ways to get
two integers that have product 80. These are
products
1 x 80 = 80
2 x 40 = 80
4 x 20 = 80
5 x 16 = 80
8 x 10 = 80
Now look at the sign of the last number in
Multiply the first number, 2, on the left by the last
number on the left, 40.
(Take these as positive).
You get 80. So we write down all the ways to get
two integers that have product 80. These are
products
1 x 80 = 80
2 x 40 = 80
4 x 20 = 80
5 x 16 = 80
8 x 10 = 80
Now look at the sign of the last number in
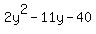 = 0, -2. It is negative, so out beside
the multiplication, subtract the smaller of the
factors from the larger factor:
[Note: if that last sign had been positive, we would add,
not subtract.]
products differences
1 x 80 = 80 80 - 1 = 79
2 x 40 = 80 40 - 2 = 38
4 x 20 = 80 20 - 4 = 16
5 x 16 = 80 16 - 5 = 11
8 x 10 = 80 10 - 8 = 2
= 0, -2. It is negative, so out beside
the multiplication, subtract the smaller of the
factors from the larger factor:
[Note: if that last sign had been positive, we would add,
not subtract.]
products differences
1 x 80 = 80 80 - 1 = 79
2 x 40 = 80 40 - 2 = 38
4 x 20 = 80 20 - 4 = 16
5 x 16 = 80 16 - 5 = 11
8 x 10 = 80 10 - 8 = 2
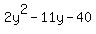 = 0
Since the middle number 11 appears as a difference
between 16 and 5, we use 16 and 5 to rewrite the
middle term "
= 0
Since the middle number 11 appears as a difference
between 16 and 5, we use 16 and 5 to rewrite the
middle term "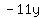 ".
We rewrite
".
We rewrite 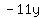 as
as 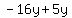 So
So 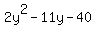 = 0
becomes
= 0
becomes
 = 0
Now factor 2y out of the first two terms on the left:
= 0
Now factor 2y out of the first two terms on the left:
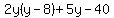 = 0
Now factor +5 out of the last two terms on the left:
= 0
Now factor +5 out of the last two terms on the left:
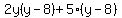 = 0
Now factor out the binomial factor
= 0
Now factor out the binomial factor 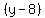
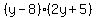 = 0
Set
= 0
Set  which gives solution
which gives solution  Set
Set  which gives solution
which gives solution  Edwin
Edwin