what is the geometric series 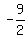 +
+ +
+ +
+ -...+
-...+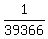 in summation notation?
in summation notation?
 We divide the 2nd term by the 1st term to find the common ratio
We divide the 2nd term by the 1st term to find the common ratio 
 To check we divide the 3rd term by the 2nd term to see if we get the
same common ratio
To check we divide the 3rd term by the 2nd term to see if we get the
same common ratio  :
:
 To double check we divide the 4th term by the 3rd term to see if we get the
same common ratio
To double check we divide the 4th term by the 3rd term to see if we get the
same common ratio  :
:
 Now that we are triple-sure that the common ratio
Now that we are triple-sure that the common ratio  ,
we will use the formula for the nth term:
,
we will use the formula for the nth term:
 to find out how many terms it has:
to find out how many terms it has:
 is the last, or nth, term:
is the last, or nth, term:
 is the first term
is the first term
 is the common ratio.
Substituting:
is the common ratio.
Substituting:
 Multiply both sides by
Multiply both sides by 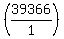

 Write
Write 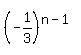 as
as 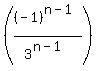
 Multiply both sides by
Multiply both sides by 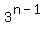 Observe that
Observe that  , so substitute that:
, so substitute that:
 Divide both sides by
Divide both sides by 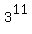
 Subtract exponents on the left:
Subtract exponents on the left:

 Since the right side is a power of
Since the right side is a power of
 , it is either 1 or -1
But no power of 3 can be negative, so
, it is either 1 or -1
But no power of 3 can be negative, so
 And since the only power of 3 that gives 1
is the 0 power, i.e., 30=1, then
the exponent n-12 must equal 0.
n-12=0
n=12.
So there are 12 terms. So
And since the only power of 3 that gives 1
is the 0 power, i.e., 30=1, then
the exponent n-12 must equal 0.
n-12=0
n=12.
So there are 12 terms. So
 becomes:
becomes:
 write
write 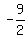 as
as 
 write
write 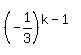 as
as 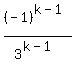
 Write
Write  as
as  :
:


 Add exponents of
Add exponents of  on top:
on top:

 Subtract exponents of 3:
Subtract exponents of 3:

 Edwin
Edwin