Question 145753: how do I solve: c^3+c^2-7c-3=0, given root -3?
Answer by nabla(475)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, note that this method is fairly advanced. If you don't understand what I'm doing, E-mail me what method you were supposed to use to solve this...
I'm going to change c to x.
By the given information we have,
(x+3)(ax^2+bx+c)=0
and if we expand this out, we have:
3 c + 3 b x + c x + 3 a x^2 + b x^2 + a x^3=0
From this and the original coefficients 1, 1, -7, -3, respectively, it follows that:
3c=-3, implies c=-1
3b+c=-7, implied 3b=-6, implies b=-2
3a+b=1, implies 3a=3, implies a=1.
We don't have to solve the cubic coefficients.
So, the original polynomial factors as:
(x+3)(x^2-2x-1)=0
Now, we can solve for the other roots by applying the quadratic formulae:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=8 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 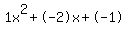 can be factored: can be factored:

Again, the answer is: 2.41421356237309, -0.414213562373095.
Here's your graph:
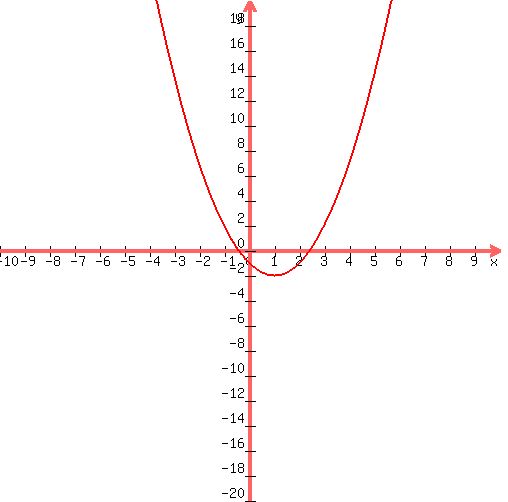 |
Which gives 
So, all zeroes are  and -3. We can see this in the following graph of the cubic: and -3. We can see this in the following graph of the cubic:

|
|
|