Question 145496: A, B, C can finish a job in 6 days. If B and C work together, the job will take 9 days if A and C work together, the job will take 8 days. In how many days can each man working alone do the job?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A, B, C can finish a job in 6 days. If B and C work together, the job will take 9 days if A and C work together, the job will take 8 days. In how many days can each man working alone do the job:
:
Write an equation for each statement.
Let the completed job = 1
:
"A, B, C can finish a job in 6 days."
 = 1 = 1
:
"If B and C work together, the job will take 9 days"
 = 1 = 1
:
"if A and C work together, the job will take 8 days."
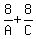 = 1 = 1
:
Use elimination: multiply equation 1 by 4 and multiply equation 3 by 3:
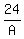 + +  + +  = 4 = 4
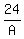 + + 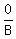 + +  = 3 = 3
--------------------------------Subtracting eliminates, A & C:
24/B = 1
B = 24 days to complete the job by himself
:
Using equation 2, substitute 24 for B
 + +  = 1 = 1
Multiply equation by 24C
9C + 9(24) = 24C
9C + 216 = 24c
216 = 24C - 9C
C = 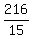
C = 14.4 days working alone
:
Use equation 3 to find A, substitute 14.4 for C
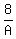 + +  = 1 = 1
Multiply eq by 14.4A
8(14.4) + 8A = 14.4A
:
115.2 = 14.4A - 8A
A = 
A = 18 days working alone
:
:
Check solution using equation 1:
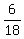 + + 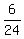 + +  = =
.333 + .250 + .417 = 1
|
|
|