|
Question 145290: I'm still having trouble with the graph method.Could someone please show me how to do a couple of my practice problems? Also when you draw the lines on the graph,could you please draw the dots first,so I can understand how you got where the lines go?
1) -x + y = -1
x + y = 3
2) 3x + y = -6
x + y = -4
I want to think you for all your help and time in advance.I think people like you are wonderful,because you help people like me that want to understand math concepts,but are still having some difficulties. Elle J
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! note: I added the solution to #2
# 1
Jump to problem #2
Once again, I'll do the first one to get you started (hopefully in the right direction)
Let's graph the first equation  . To do this, we must first solve for y . To do this, we must first solve for y
 Start with the first equation Start with the first equation
 Add Add  to both sides to both sides
 Rearrange the equation Rearrange the equation
Looking at  we can see that the equation is in slope-intercept form we can see that the equation is in slope-intercept form  where the slope is where the slope is  and the y-intercept is and the y-intercept is 
Since  this tells us that the y-intercept is this tells us that the y-intercept is ) .Remember the y-intercept is the point where the graph intersects with the y-axis .Remember the y-intercept is the point where the graph intersects with the y-axis
So we have one point )

Now since the slope is comprised of the "rise" over the "run" this means

Also, because the slope is  , this means: , this means:

which shows us that the rise is 1 and the run is 1. This means that to go from point to point, we can go up 1 and over 1
So starting at ) , go up 1 unit , go up 1 unit

and to the right 1 unit to get to the next point )

Now draw a line through these points to graph 
 So this is the graph of So this is the graph of  through the points through the points ) and and )
-----------------------------------------
Now let's graph the second equation  . To do this, we must first solve for y . To do this, we must first solve for y
 Start with the second equation Start with the second equation
 Subtract Subtract  from both sides from both sides
 Rearrange the equation Rearrange the equation
Looking at  we can see that the equation is in slope-intercept form we can see that the equation is in slope-intercept form  where the slope is where the slope is  and the y-intercept is and the y-intercept is 
Since  this tells us that the y-intercept is this tells us that the y-intercept is ) .Remember the y-intercept is the point where the graph intersects with the y-axis .Remember the y-intercept is the point where the graph intersects with the y-axis
So we have one point )
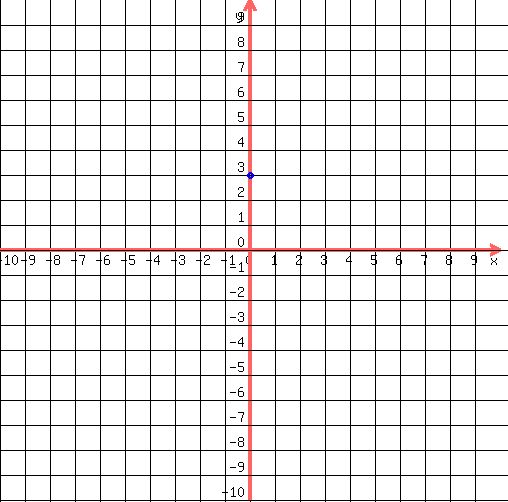
Now since the slope is comprised of the "rise" over the "run" this means

Also, because the slope is  , this means: , this means:

which shows us that the rise is -1 and the run is 1. This means that to go from point to point, we can go down 1 and over 1
So starting at ) , go down 1 unit , go down 1 unit

and to the right 1 unit to get to the next point )

Now draw a line through these points to graph 
 So this is the graph of So this is the graph of  through the points through the points ) and and )
------------------------------
Now let's graph the two equations together
 Graph of Graph of  (red) and (red) and  (green) (green)
So from the graph, we can see that the two lines intersect at the point (2,1).
# 2
Jump to problem #1
Let's graph the first equation  . To do this, we must first solve for y . To do this, we must first solve for y
 Start with the first equation Start with the first equation
 Subtract Subtract 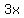 from both sides from both sides
 Rearrange the equation Rearrange the equation
Looking at  we can see that the equation is in slope-intercept form we can see that the equation is in slope-intercept form  where the slope is where the slope is  and the y-intercept is and the y-intercept is 
Since  this tells us that the y-intercept is this tells us that the y-intercept is ) .Remember the y-intercept is the point where the graph intersects with the y-axis .Remember the y-intercept is the point where the graph intersects with the y-axis
So we have one point )

Now since the slope is comprised of the "rise" over the "run" this means

Also, because the slope is  , this means: , this means:

which shows us that the rise is -3 and the run is 1. This means that to go from point to point, we can go down 3 and over 1
So starting at ) , go down 3 units , go down 3 units

and to the right 1 unit to get to the next point )

Now draw a line through these points to graph 
 So this is the graph of So this is the graph of  through the points through the points ) and and )
---------------------------------------
Let's graph the second equation  . To do this, we must first solve for y . To do this, we must first solve for y
 Start with the second equation Start with the second equation
 Subtract Subtract  from both sides from both sides
 Rearrange the equation Rearrange the equation
Looking at  we can see that the equation is in slope-intercept form we can see that the equation is in slope-intercept form  where the slope is where the slope is  and the y-intercept is and the y-intercept is 
Since  this tells us that the y-intercept is this tells us that the y-intercept is ) .Remember the y-intercept is the point where the graph intersects with the y-axis .Remember the y-intercept is the point where the graph intersects with the y-axis
So we have one point )

Now since the slope is comprised of the "rise" over the "run" this means

Also, because the slope is  , this means: , this means:

which shows us that the rise is -1 and the run is 1. This means that to go from point to point, we can go down 1 and over 1
So starting at ) , go down 1 unit , go down 1 unit

and to the right 1 unit to get to the next point )

Now draw a line through these points to graph 
 So this is the graph of So this is the graph of  through the points through the points ) and and )
------------------------------
 Graph of Graph of  (red) and (red) and  (green) (green)
So from the graph, we can see that the two lines intersect at the point (-1,-3).
|
|
|
| |