SOLUTION: What is the directrix of the parabola with the equation y+3= 1/10 (x+2)^2?

What you have to know about parabolas in standard form:

1: Parabolas whose equations are in the standard form



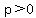opens upward if  and downward if 

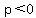They have vertex (h, k), focus (h, k+p), and
the directrix is the horizontal line whose equation
is y=k-p

2: Parabolas whose equations are in the standard form



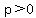opens rightward if  and leftward if 

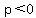They have vertex (h, k), focus (h+p, k), and
the directrix is the vertical line whose equation
is x=h-p.


Your equation



can be placed in the standard form 1.

Multiply both sides by 10







Swap sides:



Compare to the standard equation in 1 above:



So  so ,
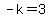 so 
 so 
opens upward because  

It has vertex (h, k) = (-2,-3)

It has focus (h, k+p) = (-2,-3+) = (-2, )
the directrix is the horizontal line whose equation
is  or  or 

To draw the graph, plot the focus (-2, ), the vertex(-2,-3) and
the directrix 

 

Draw a line from the focus directly to the directrix. The
vertex should be the midpoint of this line.



Draw a square with that line being its left side:



Draw another square with that line being its right side:



Finally, draw the parabola through the vertex and the
upper corners of the two squares:



Edwin