For each of the equations (a), (b), and (c) below, indicate which graphs represents the equation. State the domain and range
(1)  Graph: Domain Range
Graph: Domain Range
This has the graph
 Since for every point on the x-axis there is a point on the
graph which is either directly above it, directly below it,
or on it, its domain is "all real numbers", or (
Since for every point on the x-axis there is a point on the
graph which is either directly above it, directly below it,
or on it, its domain is "all real numbers", or ( ,
, )
Since for every point on the y-axis there is a point on the
graph which is either directly to the left of it, directly to the right of
it, or on it, its range is "all real numbers", or (
)
Since for every point on the y-axis there is a point on the
graph which is either directly to the left of it, directly to the right of
it, or on it, its range is "all real numbers", or ( ,
, )
)
(2)  Graph: Domain Range
Graph: Domain Range
This has the graph
 Since for every point on the x-axis there is a point on the
graph which is either directly above it, or on it, its domain is
"all real numbers", or (
Since for every point on the x-axis there is a point on the
graph which is either directly above it, or on it, its domain is
"all real numbers", or ( ,
, )
However for every point on the y-axis there is NOT ALWAYS a point on the
graph which is either directly to the left of it, directly to the right it,
or on it. So its range will include ONLY those points on the y-axis
for which there is a point on the curve directly left or directly right of it,
or on it. So its range consists of those values on the y-axis
which are either positive or 0, the origin and above. Therefore the range is
[
)
However for every point on the y-axis there is NOT ALWAYS a point on the
graph which is either directly to the left of it, directly to the right it,
or on it. So its range will include ONLY those points on the y-axis
for which there is a point on the curve directly left or directly right of it,
or on it. So its range consists of those values on the y-axis
which are either positive or 0, the origin and above. Therefore the range is
[ ,
, )
)
(3)  Graph: Domain Range
Graph: Domain Range
This has the graph
 Since for every point on the x-axis there is a point on the
graph which is either directly above it, or on it, its domain is
"all real numbers", or (
Since for every point on the x-axis there is a point on the
graph which is either directly above it, or on it, its domain is
"all real numbers", or ( ,
,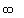 )
However for every point on the y-axis there is NOT ALWAYS a point
on the graph which is either directly to the left of it, directly
to the right it, or on it. So its range will include ONLY those
points on the y-axis for which there is a point on the curve
directly left of it, directly right of it, or on it. So its range
consists of only those points on the y-axis which are at 1 or lower.
So the range is (
)
However for every point on the y-axis there is NOT ALWAYS a point
on the graph which is either directly to the left of it, directly
to the right it, or on it. So its range will include ONLY those
points on the y-axis for which there is a point on the curve
directly left of it, directly right of it, or on it. So its range
consists of only those points on the y-axis which are at 1 or lower.
So the range is ( ,
, ]
Edwin
]
Edwin