Question 145137: Find the equation of an ellipse with its center at (1,2), focus at (6, 2) and containing the point (4,6).
I have so far (x-1)^2 + (y-2)^2 = 1, but I cannot figure out what my a^2 and b^2 should be for my denominators. Please help.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation of an ellipse with its center at (1,2), focus at (6, 2) and containing the point (4,6).
Since the center and focus have the same y-value,
we know this is an ellipse whose major axis is
horizontal, so its equation is in the form:
 The center is (
The center is ( , , )
The left focus is ( )
The left focus is (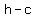 , , ) and the
right focus is ( ) and the
right focus is (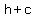 , , ), where ), where  ---------------------------------------------
We substitute the center (h,k) = (1,2)
---------------------------------------------
We substitute the center (h,k) = (1,2)
 We substitute the given point (x,y) = (4,6)
We substitute the given point (x,y) = (4,6)


 The focus given (
The focus given ( , , ) must be a right focus
since ( ) must be a right focus
since ( , , ) is right of the center ( ) is right of the center ( , , ), so
( ), so
(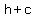 , , ) = ( ) = ( , , )
So )
So  and of course and of course  and since and since 

 Now using the fact that
Now using the fact that  substituting substituting  : :


 So we have this system of equations:
So we have this system of equations:

 Can you solve that for
Can you solve that for  and and  by substitution?
If not post again asking how.
You get by substitution?
If not post again asking how.
You get  and and  Substituting in
Substituting in

 Edwin
Edwin
|
|
|