The force needed to keep a car from skidding on a curve varies jointly as the weight of the car and the square of the car's speed, and inversely as the radius of the curve. If a force of 3600 pounds is needed to keep an 1800 pound car traveling at 20 mph from skidding on a curve of radius 600 feet what force would be required to keep the same car from skidding on a curve of radius 570 feet at 50 mph? Round to the nearest pound of force.
This is the general formula for all variation problems:

>>...The force needed to keep a car from skidding on a curve varies...<<
This force is the 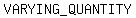 . We will use the letter
. We will use the letter  . So
. So

>>...jointly as the weight of the car and the square of the car's speed,...<<
The 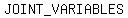 are the weight,
are the weight,  , and speed,
, and speed,  , squared, which gives
, squared, which gives 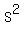
>>...and inversely as the radius of the curve...<<
There is just one 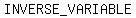 , the radius
, the radius  .
So we write the equation using the general formula for all
variation problems:
.
So we write the equation using the general formula for all
variation problems:
 eliminating the ones that don't apply:
eliminating the ones that don't apply:


>>...If a force of 3600 pounds is needed to keep an 1800 pound car traveling at 20 mph from skidding on a curve of radius 600 feet...<<
Plug those values in:  ,
, ,
,  ,
, 

 Solve for k:
Solve for k:

 So go back to this equation:
So go back to this equation:
 and substitute only the value of
and substitute only the value of 
 or we can just make it
or we can just make it
 Now our formula is complete. We are now ready to use it:
Now our formula is complete. We are now ready to use it:
>>...what force would be required to keep the same car
from skidding on a curve of radius 570 feet at 50 mph?...<<
That just asks: What is  when
when  ,
,  , and
, and  So we plug those in:
So we plug those in:



>>...Round to the nearest pound of force...<<
we round that to the nearest pound.
 Edwin
Edwin