Question 144794: How many ways can 4 people be chosen from a group of 9? Tell wheater the situation is permutation or combination
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! It depends. Does the order of the group of 4 people matter? Let's say your group of 9 consists of Alice, Bob, Carly, David, Ernest, Fran, Gillian, Henry, and Iris. Clearly, Alice, Bob, Carly, and David is one set of 4 people that you could select. The question is this: Is Alice, Bob, Carly, and David different from David, Carly, Bob, and Alice? If you were just selecting 4 committee members, then the order doesn't matter, but if you were selecting a Club President, Vice-President, Secretary, and Treasurer, then order would definitely matter.
So, if order matters, then you have a permutation of 9 things taken 4 at a time given by: 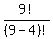 . Here's a calculation shortcut: . Here's a calculation shortcut:  . .
If order does not matter, then you have a combination, and the answer you got for the permutation is too large by a factor of the number of ways that you can arrange the group of 4, namely 4!. So you need to divide the permutation calculation by that amount: The combination of 9 things taken 4 at a time is then: 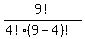 . Use the same calculation shortcut from above: . Use the same calculation shortcut from above:
 . .
|
|
|