Question 144493This question is from textbook Algebra 2 (California Edition)
: A shipment of ten television sets contains 3 defective sets. How many ways can a hospital purchase 4 of these sets and recieves at least 2 of the defective sets?
This question is from textbook Algebra 2 (California Edition)
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! This problem might be easier to approach if you
ask the opposite question:
"How many ways can the hospital purchase 4 of the 10
sets and only get 1 of the defective sets or none of
the defective sets?"
If I don't get any defective sets, then there are
7 possible sets for the 1st one, 6 possible sets for
the 2nd one, 5 for the 3rd, and 4 for the 4th
The number of different combinations is 
----------------------------------
If I know I'm going to have 1 defective set, that means
I don't have 4 to choose from for the last set, I only
have the 3 defective ones, so the number of combinations
with 1 defective set is 
----------------------------------
Then I have to ask, "If I include ALL the possible combinations
whether a set is defective or not, how many combinations
are there? That answer is: 
-----------------------------------
Now if I add  and  , I get the number of combinations
that I DON'T want 
-----------------------------------
My answer should be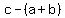 
If I'm right, there are 3570 different combinations of 4 sets that
include at least 2 defective ones. As with any problem like this,
reasoning can off, so see if you agree.
-----------------------------------
I thought this one over, and decided that I solved
for all possible ARRANGEMENTS of the TVs in question, as if it
made a difference which came 1st, 2nd, etc, which it doesn't
So change to
Change to
Change  to
There are 70 different combinations of 4 sets that
include at least 2 defective ones.
Of course, unless I'm wrong again. Check the answer.
|
|
|
