Question 144445: Steve traveled 200 miles at a certain speed. Had he gone 10 mph faster, the trip would have taken 1 hour less. Find the speed of his vehicle.
How would you turn this into an algebraic equation and solve it. I'm sorry if i seem to be a total idiot. But i have no CLUE. Please help me someone!!
Found 2 solutions by stanbon, Alan3354:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Steve traveled 200 miles at a certain speed. Had he gone 10 mph faster, the trip would have taken 1 hour less. Find the speed of his vehicle.
---------------
Before speed change DATA:
distance = 200 miles ; speed = x mph ; time = d/r = 200/x hrs.
----------------------------
After speed change DATA:
distance = 200 miles ; speed = "x+10" mph ; time = d/r = 200/(x+10)
-----------------------------
EQUATIOn:
original time - new time = 1 hr
200/x - 200/(x+10) = 1
200x+ 2000 - 200x = x(x+10)
x^2+10x-2000 = 0
(x+50)(x-40) = 0
Positive solution:
x = 40 mph (original speed)
x + 10 = 50 mph (newspeed)
=============================
Cheers,
Stan H.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Tricky problem.
Call the speed S and the time H (for hours).
The distance is 200, and is Speed x Hours, S times H.
Going faster takes less time. 200 = (S + 10) times (H-1)
We have 2 equations in 2 unknowns now.
SH = 200 eqn 1
(S+10)(H-1) = 200 eqn 2
SH + 10H -S -10 = 200, or
SH + 10H -S -10 = SH
10H -S -10 = 0
S = 200/H
10H - 200/H - 10 = 0
Multiply by H

Divide by 10

| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=81 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 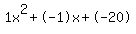 can be factored: can be factored:

Again, the answer is: 5, -4.
Here's your graph:
 |
H = 5, or -4. -4 hours makes no sense, so it's discarded.
The time is 5 hours to go 200 miles. So the speed is 40 mph
Going 50 mph would take 4 hours, so the answer is correct.
|
|
|