Question 144427: Please help me solve this equation: 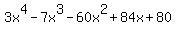
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! What equation? I don't see an equals sign anywhere, and you can't have an equation without an equals sign. What you have provided is a quartic function. If you actually meant that you want to find the zeros of the quartic, that is to say you want to solve  , then I would proceed first with the Rational Zero Theorem to check for possible rational zeros. , then I would proceed first with the Rational Zero Theorem to check for possible rational zeros.
Rational Zero Theorem
If a polynomial function, written in descending order, has integer coefficients, then any rational zero must be of the form ± p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.
Once you have determined all of the possible rational zeros, use polynomial long division or synthetic division to divide 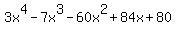
by  where where  is one of the possible rational zeros. Continue this process until you find one of the possibilities that divides evenly, i.e. no remainder, or you have exhausted all the possibilities. is one of the possible rational zeros. Continue this process until you find one of the possibilities that divides evenly, i.e. no remainder, or you have exhausted all the possibilities.
If you find one that divides evenly, you have found one of the 4 zeros of the quartic, and you have reduced the difficulty of your problem because you now can find the other three solutions by finding the zeros of the cubic polynomial that is the quotient resulting from the division. Apply the Rational Zero Theorem to this cubic...yada yada yada. Then when you find a root of the cubic, your quotient will be a quadratic that you can solve with the quadratic formula or by factoring if possible.
On the other hand, if you are unable to find any rational zeros because you have tried every possiblity determined in your first application of the Rational Zero Theorem, you must then go through the process of solving the general quartic. See Quartic Equations in Wikipedia -- there is a nice dissertation on the subject and a description of the process of solving the general quartic. The good news is that if you DO find a rational zero for the quartic, then there must also be one for the resulting cubic. That is because both complex and irrational zeros of polynomials come in conjugate pairs. Two of the zeros for the cubic might be either complex or irrational (including complex with irrational coefficients) but one of them cannot be paired and therefore must be rational.
I did a little investigating and have discovered that there is, in fact, a rational zero for your original quartic. Thank goodness, because the general solution for the quartic is a horror that I wouldn't even wish on someone I DIDN'T like.
|
|
|