Question 144278: Please help me solve: There are 50 dimes in a roll of dimes, 40 nickles in a rold of nickels, and 40 quarters in a roll of quarters. Robert has a total of 12 rolls of coins wiht the total value of $70. If he has 3 more rolls of nickles than dimes, how many of each roll of coins does he have?
Found 2 solutions by Alan3354, ankor@dixie-net.com:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are 50 dimes in a roll of dimes, 40 nickels in a roll of nickels, and 40 quarters in a roll of quarters. Robert has a total of 12 rolls of coins with the total value of $70. If he has 3 more rolls of nickels than dimes, how many of each roll of coins does he have?:
:
total no. of rolls equation
n + d + q = 12
;
$Value equation:
.05(40n) + .10(50d) + .25(40q) = 70
:
2n + 5d + 10q = 70
:
"he has 3 more rolls of nickels than dimes,"
n = (d+3)
:
Replace n with (d+3) in both equations:
(d+3) = d + q = 12
2d + q = 12 - 3
2d + q = 9
and
2(d+3) + 5d + 10q = 70
2d + 6 + 5d + 10q = 70
7d + 10q = 70 - 6
7d + 10q = 64
:
Two equations, two unknowns, we can handle that, can't we.
Multiply the 1st two unknown eq by 10, subtract the 2nd one
20d + 10q = 90
7d + 10q = 64
-----------------subtracting eliminates q, find d
13d + 0q = 26
d = 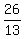
d = 2 rolls of dimes
:
See if you can find the no. of rolls of nickels and quarters now.
Check your solutions in the $value equation.
If you have difficulty, email me: ankor@dixie-net.com
|
|
|