Question 144172: Given: triangle ABC A(-1,2) B(7,0) C(1,-6) and a point D(4,-3) on segment BC
Prove: segment AD is the perpendicular bisector of segment BC
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given: triangle ABC A(-1,2) B(7,0) C(1,-6) and a point D(4,-3) on segment BC
Prove: segment AD is the perpendicular bisector of segment BC
 First we use the midpoint formula to show that D
is the midpoint of BC. That will show that AD is
a bisector of BC. Then we will use the slope
formula to show that AD is perpendicular to BC.
The midpoint of the segment joining (
First we use the midpoint formula to show that D
is the midpoint of BC. That will show that AD is
a bisector of BC. Then we will use the slope
formula to show that AD is perpendicular to BC.
The midpoint of the segment joining (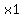 , ,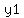 ) and ( ) and (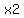 , ,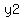 ) is
given by the formula ) is
given by the formula
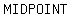 = ( = (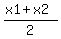 , ,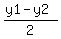 )
We use B( )
We use B( , , ) as ( ) as (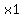 , ,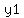 )
and C( )
and C( , , ) as ( ) as (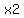 , ,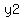 ) )
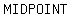 = ( = ( , , ) )
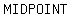 = ( = (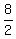 , ,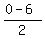 ) )
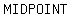 = ( = ( , ,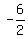 ) )
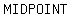 = ( = ( , , )
Since D has those coordinates, AD bisects BC.
Now we need to show AD and BC are perpendicular.
The slope of the segment joining ( )
Since D has those coordinates, AD bisects BC.
Now we need to show AD and BC are perpendicular.
The slope of the segment joining (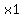 , ,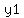 ) and ( ) and (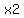 , ,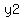 ) is
given by the formula ) is
given by the formula
 So we now find the slope of BC, again using
B(
So we now find the slope of BC, again using
B( , , ) as ( ) as (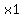 , ,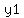 )
and C( )
and C( , , ) as ( ) as (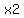 , ,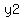 ) )



 So the slope of BC is
So the slope of BC is  Now So we now find the slope of AD, using
A(
Now So we now find the slope of AD, using
A( , , ) as ( ) as (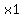 , ,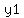 )
and D( )
and D( , , ) as ( ) as (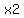 , ,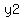 ) )



 So the slope of AD is
So the slope of AD is  Since
Since  and and  are reciprocals with
opposite signs, this proves AD is perpendicular to
BC.
Therefore AD is the perpendicular bisector of BC.
Edwin are reciprocals with
opposite signs, this proves AD is perpendicular to
BC.
Therefore AD is the perpendicular bisector of BC.
Edwin
|
|
|