SOLUTION: How would I solve the below problem...THX tutors!!! :) log(16)X + log(8)X + log(4)X + log(2)X = 6 (the 16, 8, 4, and 2 are all smaller numbers)

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: How would I solve the below problem...THX tutors!!! :) log(16)X + log(8)X + log(4)X + log(2)X = 6 (the 16, 8, 4, and 2 are all smaller numbers)       Log On


   

Question 143986: How would I solve the below problem...THX tutors!!! :)
log(16)X + log(8)X + log(4)X + log(2)X = 6
(the 16, 8, 4, and 2 are all smaller numbers)
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Use the rule for base conversion: log%28n%2Cx%29=%28log%28b%2Cx%29%29%2F%28log%28b%2Cn%29%29

So: log%2816%2Cx%29=%28log%282%2Cx%29%29%2F%28log%282%2C16%29%29, but since we know that if log%28b%2Cx%29=y then b%5Ey=x, so log%282%2C16%29=y means that 2%5Ey=16. Solving for y gives us y=4, so log%282%2C16%29=4. That means that log%2816%2Cx%29=%28log%282%2Cx%29%29%2F4.

Using a similar process, we get:

log%288%2Cx%29=%28log%282%2Cx%29%29%2F3 and log%284%2Cx%29=%28log%282%2Cx%29%29%2F2

Now we can write:


Applying the common denominator of 12:


Simplifying:
25%2Alog%282%2Cx%29=72
log%282%2Cx%29=2.88

Therefore x=2%5E%282.88%29

That is the exact answer. You can use the x^y function on your Windows calculator in scientific mode to calculate a numerical approximation.

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
How would I solve the below problem...THX tutors!!! :)
log%2816%2Cx%29+%2B+log%288%2Cx%29+%2B+log%284%2Cx%29+%2B+log%282%2Cx%29+=+6 

Use the 'change of base' formula:



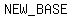
on each of the first three terms on the left, using 2 as the NEW_BASE


 
Now we can evaluate those three denominators by using the definition of
logarithm:

   log%28B%2CA%29=C is equivalent to B%5EC=A

For log%282%2C16%29, we set it equal to the unknown "y":

log%282%2C16%29=y

Then it is equivalent to 2%5Ey=16 or 2%5Ey=2%5E4, so y+=+4,
therefore log%282%2C16%29=y=4  

------

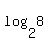For log%282%2C8%29, we set it equal to the unknown "z":

log%282%2C8%29=z

Then it is equivalent to 2%5Ez=8 or 2%5Ez=2%5E3, so z+=+3,
therefore log%282%2C8%29=z=4 

------

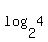For log%282%2C4%29, we set it equal to the unknown "w":

log%282%2C4%29=w

Then it is equivalent to 2%5Ew=4 or 2%5Ew=2%5E2, so w+=+2,
therefore log%282%2C4%29=w=2 

------

Substitute these for the first three terms of:



log%282%2Cx%29%2F4+%2B+log%282%2Cx%29%2F3+%2B+log%282%2Cx%29%2F2+%2B+log%282%2Cx%29+=+6

Clear of fractions by multiplying every term by LCD = 12



3log%282%2Cx%29+%2B+4log%282%2Cx%29+%2B+6log%282%2Cx%29+%2B+12log%282%2Cx%29+=+12%2A6

%283%2B4%2B6%2B12%29log%282%2Cx%29+=+72

25%2Alog%282%2Cx%29+=+72

Divide both sides by 25

25%2Alog%282%2Cx%29%2F25+=+72%2F25

log%282%2Cx%29+=+72%2F25

Now use the definition of logarithm again to rewrite
that as

drawing%2850%2C50%2C0%2C2%2C-3%2C2%2C+locate%280%2C0%2Cx=2%5E%2872%2F25%29%29+%29

Find that on a TI calculator by typing 

2^(72/25)

then pressing ENTER

x+=+7.361501205  

Edwin