Question 143235: I am completely confused regarding trig, the beginner trig in involving right triangles:
Sin: opposite leg/ hypotenuse
Cos: adjacent leg/ hypotenuse
Tan: adjacent leg/opposite leg
Is this correct?
How do you know what leg is adjacent?
What happens when you have a angle but you need to find a leg number? Do you use 'sin-1'?
Found 3 solutions by vleith, jim_thompson5910, solver91311:
Answer by vleith(2983)   (Show Source): (Show Source):
You can put this solution on YOUR website! Tangent = opposite/adjacent
See here for a good picture --> http://www.grc.nasa.gov/WWW/K-12/airplane/sincos.html
When thinking about sine, cosine and tangent, one has to think about which vertex of the triangle you are referencing. Assume you pick one vertex, then the adjacent leg is the one that 'touches' your vertex. The hypotenuse is always the 'long side'. make sense?
When you have an angle, and also one of the sides (but not a second side), you setup the ratios as you nothed above, and then use your calculator to find the sine or cosine ro tangent of the angle. The cross multiply to find the unknown side.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your function definitions are correct.
If you have a right triangle, then you have one right angle and two other (acute) angles. The two acute angles are each formed by the hypotenuse and one of the legs. That leg that forms one side of the angle is the adjacent side, and the other leg is the opposite side. The way to remember is that the word adjacent means 'next to' So the adjacent side is 'next to' the angle, and the opposite side is across from or 'opposing' the angle.
See figure:
Side c is the hypotenuse.
Side a is opposite Angle A and Side b is adjacent Angle A
Side b is opposite Angle B and Side a is adjacent Angle B

If you know the measure of an angle and the measure of the length of any of the three sides, then you can calculate all of the other parts. Knowing just the measure of one of the acute angles is insufficient information because there are an infinite number of similar right triangles with the given acute angle measure.
Let's say you know (refering to the figure) Angle a and Side b, and you want to find the hypotenuse.
Knowing that  , you can look up (or use your calculator) to find , you can look up (or use your calculator) to find  and divide that into and divide that into  (the measure of the adjacent side) to get the measure of the hypotenuse. (the measure of the adjacent side) to get the measure of the hypotenuse.
Where you would use the inverse functions  , , ,and ,and  is when you are given the measures of two of the sides and want to know the angle. ( is when you are given the measures of two of the sides and want to know the angle. ( , meaning 'arcsin' is the same as 'inverse sin' or sin raised to the -1 power) When you see , meaning 'arcsin' is the same as 'inverse sin' or sin raised to the -1 power) When you see  read it like this: "The measure of the angle whose sine is x" For example, let's say (referring to the figure) you are given the measures of sides read it like this: "The measure of the angle whose sine is x" For example, let's say (referring to the figure) you are given the measures of sides  and and  and are asked to find the measure of Angle and are asked to find the measure of Angle 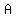 . If you divide . If you divide  (the opposite side) by (the opposite side) by  (the hypotenuse), you get the value of (the hypotenuse), you get the value of  . Now you need to use . Now you need to use  to find the measure of the angle whose sine is to find the measure of the angle whose sine is 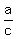 . .
|
|
|