Question 143151: sketch a graph of each rational function. Show all asymptotes and/or holes.
1. y=(4)/(x^2-1)
2. y=(3x)/(x^2-3x)
Answer by nabla(475)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, simplify each equation a little:

This tells us right away that x cannot equal +/- 1!!! (No dividing by zero.) Moreover, the lines x=1 and x=-1 will be vertical asymptotes. Now, for horizontal asymptotes, we must consider the degree of the x term in the numerator compared to the denominator. That is, 0 compared with 2. Since 0<2 we will have a horizontal asymptote at y=0.
Now, having already said that the denominator cannot be zero, we can say that there will be NO x-intercepts (because the denominator is the only part with x-terms). Y-intercept is easily found, however:
f(0)=4/(-1)=-4. So (0,-4) is the y-intercept. I now have enough information to plot, however you may want to write out some points to test.
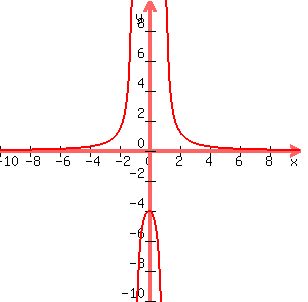
Note that the method this site uses to graph inaccurately draws vertical lines where the vertical asymptotes are. Do not include this on your graph.
#2. 
Much of the same applies here process-wise as in#1. x=3 is the vertical asymptote, y=0 is the horizontal asymptote, (0,-1) is the y-intercept.
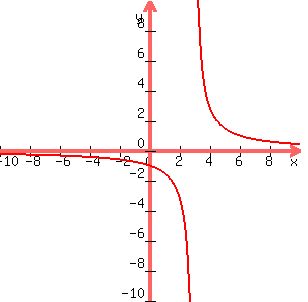
|
|
|