SOLUTION: Use the given information to find {{{sin 2(phi)}}}, {{{cos 2(phi)}}}, {{{tan 2(phi)}}}. 1. {{{tan(phi)=1/2}}}, {{{pi < phi <= (3pi/2)}}} 2. {{{sec(phi)=-5/2}}},{{{pi/2 < phi

Algebra ->  Trigonometry-basics -> SOLUTION: Use the given information to find {{{sin 2(phi)}}}, {{{cos 2(phi)}}}, {{{tan 2(phi)}}}. 1. {{{tan(phi)=1/2}}}, {{{pi < phi <= (3pi/2)}}} 2. {{{sec(phi)=-5/2}}},{{{pi/2 < phi       Log On


   

Question 142454: Use the given information to find 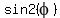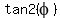sin+2%28phi%29, cos+2%28phi%29, tan+2%28phi%29.
1. tan%28phi%29=1%2F2, pi+%3C+phi+%3C=+%283pi%2F2%29
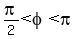
2. sec%28phi%29=-5%2F2,pi%2F2+%3C+phi+%3C+pi
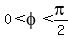
3. sin%28theta%29=3%2F5, 0+%3C+phi+%3C+pi%2F2
Any help is greatly appreciated.
Thanks,
Justin
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Use the given information to find 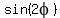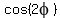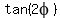sin%282phi%29, cos%282phi%29, tan%282phi%29. 

Formulas needed are

sin%282phi%29=+2sin%28phi%29cos%28phi%29 
cos%282phi%29=2cos%5E2%28phi%29-1
tan%282phi%29=sin%282phi%29%2Fcos%282phi%29+

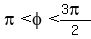1. tan%28phi%29=1%2F2, pi+%3C+phi+%3C+%283pi%29%2F2%29 

That's the THIRD quadrant.

Draw a picture of angle theta in the third quadrant

Since TANGENT+=+%28OPPOSITE%29%2F%28ADJACENT%29+=+y%2Fx 

If theta were in the first quadrant, we'd let the 
numerator of 1%2F2 be y and the denominator of 
1%2F2 be x.  But since theta is in the third 
quadrant, we have to make x and y both negative.  
So take y, the opposite, as the negative of the 
numerator, -1, and take x to be the negative of 
the denominator, -2. 

So plot the point (-2,-1) in the third quadrant and 
draw a radius to it and draw a perpendicular up to 
the x-axis, forming a right triangle:



Next we need to find r, the hypotenuse. We use the
Pythagorean theorem:

r%5E2=x%5E2%2By%5E2

r%5E2=%28-2%29%5E2%2B%28-1%29%5E2

r%5E2=4%2B1

r%5E2=5

r=sqrt%285%29

So we label that:



Now we have x=-2,y=-1,r=sqrt%285%29
And so 
sin%28phi%29=y%2Fr=%28-1%29%2F%28sqrt%285%29%29=-sqrt%285%29%2F5
cos%28phi%29=y%2Fr=%28-2%29%2F%28sqrt%285%29%29=-2sqrt%285%29%2F5

Substituting in

sin%282phi%29=+2sin%28phi%29cos%28phi%29 
sin%282phi%29=+2%28-sqrt%285%29%2F5%29%28-2sqrt%285%29%2F5%29
sin%282phi%29=+2%282%285%29%29%2F25+=+20%2F25=4%2F5++

Substituting in

cos%282phi%29=2cos%5E2%28phi%29-1
cos%282phi%29=2%28%28-2sqrt%285%29%29%2F5%29%5E2-1
cos%282phi%29=2%28+4%2A5+%29%2F25+%29-1
cos%282phi%29=40%2F25-1
cos%282phi%29=8%2F5-1
cos%282phi%29=8%2F5-5%2F5
cos%282phi%29=3%2F5

Substituting those values in:
tan%282phi%29=sin%282phi%29%2Fcos%282phi%29+
tan%282phi%29=%284%2F5%29%2F%283%2F5%29+
tan%282phi%29=%284%2F5%29%285%2F3%29
tan%282phi%29=%284%2Fcross%285%29%29%28cross%285%29%2F3%29
tan%282phi%29=4%2F3

If I have time I'll come back and do the others.

Edwin