Question 142052: Identify vertex, focus, directrix, axis of symmetry and latus rectum from the following parabola equation:

Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Identify vertex, focus, directrix, axis of symmetry and latus rectum from the following parabola equation:

Two things you must know about parabolas, their graphs
and their equations
1. The parabola whose equation is

opens upward if p is positive, and downward if p is negative.
It has:
vertex, the point (h,k),
focus, the point (h,k+p),
directrix, the horizontal line whose equation is y=k-p
length of latus rectum = 4p,
endpoints of the latus rectum, the points (h-2p,k+p),(h+2p,k+p)
2. The parabola whose equation is

opens to the right if p is positive, and
to the left if p is negative.
It has:
vertex, the point (h,k),
focus, the point (h+p,k),
directrix, the vertical line whose equation is x=h-p
length of latus rectum = 4p,
endpoints of the latus rectum, the points (h+p,k-2p),(h+p,k+2p)
Your parabola is the second type:

or

Compare that to

 so so 
 so so 
 so so 
It opens to the right because  , a positive number. , a positive number.
It has:
vertex, the point (h,k) = ( , , ) )
focus, the point (h+p,k) = (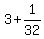 , , ) = ( ) = (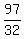 , , ) )
directrix, the vertical line whose equation is  or or  or or 
length of latus rectum = 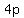 = = 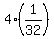 = = 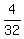 = = 
endpoints of the latus rectum, the points ( , , ) and ( ) and ( , ,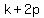 ), or ( ), or (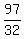 , ,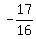 ) and ) and 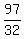 , ,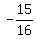 ) )
The parabola looks like this. The vertical line is the directrix.
The focus is the little dot just inside the parabola. I won't try to
draw the latus rectum. It is a very short line, only  of a of a
unit that goes across the parabola through the focus.

Edwin
|
|
|