SOLUTION: Solve for X, Y, and Z in the following systems of three equations: Can you show me the steps? a. X + Y + 2Z = 5 X + Y = 5 X + 3Y + Z = 11 b. X + 10Y +

There are at least 5 different ways to solve systems of equations.
If I pick one way, it would likely not to be the one you are 
studying.

Here are just the correct answers

(x,y,z)=(2,3,0)
(x,y,z)=(2,5,0)
(x,y,z)=(,,)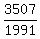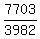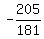

(That's the correct ugly answer for what you posted for
the third problem.  Are you sure you copied it right?
The others came out with all whole number answers, and 
this one came out with such god-awful fractions!)

Post again or email me telling the method you are studying, and
I'll show you the steps. 

Here are the 5 most common methods studied. 

1. By elimination and substitution
2. By Cramer's rule using determinants 
3. By the triangular method
4. By Gaussian elimination using the 
row echelon form of the augmented matrix
5. By Gaussian elimination using the
row reduced echelon form of the 
augmented matrix.
6. By the inverse matrix method.

Edwin