Question 141492This question is from textbook Beginning Algebra
: I need help !!!!!! :( I have to factor this one if possible. be sure to factor completely...always factor out the greatest common factor first, if one exists...
Page 336
#14
y^2+16y+64
This question is from textbook Beginning Algebra
Found 2 solutions by scott8148, solver91311:
Answer by scott8148(6628)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 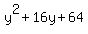
First, there are no common factors, aside from 1 which is trivial.
Remember the FOIL process to multiply two binomials, 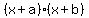 . .
First gives you: x times x or 
Outside gives you: x times b or 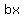
Inside gives you: x times a or 
Last gives you: a times b or 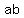
When you put the terms back together you get 
So for your problem, the trick is to find two numbers a and b so that when you multiply them together they make 64, but when you add them they make 16.
First thing to do is look at the signs in your trinomial. All of them are positive, so you know that you are looking for positive number factors. (if the sign on the constant term is + but the sign on the 1st degree term is -, then you know you are looking for two negative number factors. If the sign on the constant term is -, then the factors must be opposite signs and the larger of the two must have the same sign as the 1st degree term)
Possible factors of 64:
 , but , but 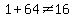
 , but , but 
 , but , but 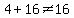
 , Aha!!!, , Aha!!!, 
So, your factors are 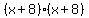 . A nice, tidy perfect square that you could also express as . A nice, tidy perfect square that you could also express as 
|
|
|