SOLUTION: Determine the equation of the line passing through the centres of the circles {{{(x-2)^2+(y+5)^2=16}}} and {{{3x^2+3y^2+24x-6y-24=0}}}

We will first find the center of each circle and 
then find the equation of the line through them.

The first one is in standard form 
and the second one is in general form:

The first equation is already in standard form



we compare it to:



So h=2, k=-5, r=4, and the center is (h,k) = (2,-5)

The second equation is not in standard form, so we
must get it in standard form also:



Divide every term by 3:



Get the x terms together, and the
y-terms together and put blanks
to add something to both sides



Complete the square on the x terms:

Take the coefficient of x, which is 8
Multiply it by , getting 4
Square what you get, 
Add that in the first blanks on both sides



Complete the square on the y terms:

Take the coefficient of y, which is -2
Multiply it by , getting -1
Square what you get, 
Add that in the remaining blanks of both sides



Combine the terms on the right:



Factor the first three terms on the left as
a perfect square:



That is in standard form, so we compare it to:



So h=-4, k=1, r=5, and the center is (h,k) = (-4,1)

So now we just need to find the line passing through
the points (2,-5) and (-4,1)

Find the slope using





Now we use the point-slope form:











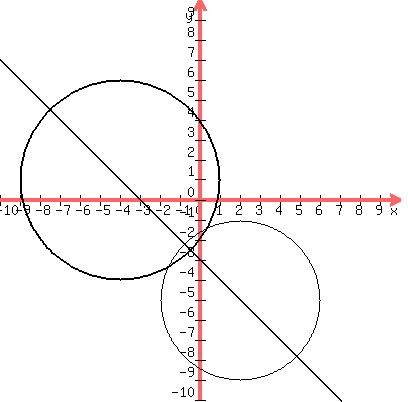
Plotting the circles and the line:



Edwin