SOLUTION: Please help me solve this simultaneous equation: log x base 3 = y = log (2x-1) base 9 and another one: log (x+y) = 0 2 log x = log (y+1)

Write two separate equations:




Use this principle to rewrite each: 
                 can be rewritten as 

Rewriting the first:


Rewriting the second:


Now rewrite  as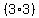 



or, multiplying exponents:



So now we have this system:




Using the second, we can substitute
 for 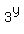 in the first:





Get 0 on the left



Factor the right side:



Using the zero factor principle,

 gives 
 gives 

So there is only one value for ,
which is 

Substitute  for x in 



Now we use the rule:
            Any number raised to the zero power, 
            except zero itself, equals 1

Thus 

and the solution is , 

Let's check:





 can be rewritten as  which is true.
 can be rewritten as  which is also true.

-------------------------------

and another one:




When no base is written, the base  is understood:




We can rewrite the first using the rule:
          can be rewritten as 
         

becomes



We can use this rule on the left side of the second eq:
                      


becomes


Now we use the principle: 
                 can be rewritten 



So we have the system of ewquations:



          
Can you solve that system of equations by substitution?
If not post again asking how.

That last system of equations has two ordered pairs 
of solutions:

(,)= (,) and (,) = (,)

However we must check them, because sometimes a solution
to our final equations is not a solution to the original
equation:

Checking (,)= (,) in the first equation:






Checking (,)= (,) in the second equation:





Since 



----

Checking (,)= (,) in the first equation:






Checking (,)= (,) in the second equation:



We can stop here because the first term is 
undefined because the logarithm of a negative 
number is not defined (except in certain 
advanced mathematics, but never in
ordinary algebra)

So there is but one solution, (,)= (,)

Edwin