Then until you get used to cubes and higher exponents
just get rid of all exponents first and write  as
as 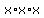 and
and  as
as 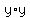 , etc.
Also break
, etc.
Also break  into a product of primes
and write it as as
into a product of primes
and write it as as 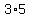 So,
So,
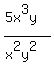 .
.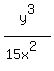 becomes
becomes
 .
.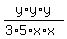 Indicate the multiplication of the numerators and
the denominators so that you only have one
fraction:
Indicate the multiplication of the numerators and
the denominators so that you only have one
fraction:
 Now cancel:
Now cancel:
 So all that's left is
So all that's left is
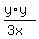 and we write
and we write 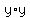 as
as  and end up with
and end up with
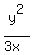 This method will always work, and you can use it
until you can see that it's quicker just to subtract
the exponents, which would amount to subtracting
the number of
This method will always work, and you can use it
until you can see that it's quicker just to subtract
the exponents, which would amount to subtracting
the number of  's or
's or  's which would
cancel in the mathod shown above.
Edwin
's which would
cancel in the mathod shown above.
Edwin