What is the vertex and focus of the parabola whose equation is
 ?
?
You must memorize:
"U-parabolas"
Parabolas which open upward or downward have equation:
 with vertex (
with vertex ( ,
, ), focus (
), focus ( ,
,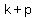 ),
the horizontal line which is the directrix has the
equation
),
the horizontal line which is the directrix has the
equation  .
the vertical line which is the axis of symmetry has the
equation
.
the vertical line which is the axis of symmetry has the
equation  .
If p is positive the parabola opens upward. If p is
negative the parabola opens downward
-----
C-parabolas
Parabolas which open rightward or leftward have equation:
.
If p is positive the parabola opens upward. If p is
negative the parabola opens downward
-----
C-parabolas
Parabolas which open rightward or leftward have equation:
 with vertex (
with vertex ( ,
, ), focus (
), focus ( ,
, ),
the vertical line which is the directrix has the
equation
),
the vertical line which is the directrix has the
equation  .
the horizontal line which is the axis of symmetry has the
equation
.
the horizontal line which is the axis of symmetry has the
equation  .
If p is positive the parabola opens rightward. If p is
negative the parabola opens leftward.
----
.
If p is positive the parabola opens rightward. If p is
negative the parabola opens leftward.
----
 we compare this to
we compare this to
 , so the parabola opens right or left
, so the parabola opens right or left
 so
so 
 so
so 
 so
so  , a negative number, so the
parabola opens left
So the vertex is (
, a negative number, so the
parabola opens left
So the vertex is ( ,
, ) = (4,8)
The focus is (
) = (4,8)
The focus is ( ,
,  ) = (
) = (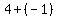 ,
, ) = (
) = (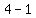 ,
, ) = (
) = ( ,
, )
the vertical line which is the directrix has the
equation
)
the vertical line which is the directrix has the
equation  , or
, or  or
or  or
or  the vertical line which is the axis of symmetry has the
equation
the vertical line which is the axis of symmetry has the
equation  , or
, or  .
To draw the parabola, plot the focus, vertex, and directrix
.
To draw the parabola, plot the focus, vertex, and directrix
 Draw a line from the focus thru to vertex to the directrix.
Draw a line from the focus thru to vertex to the directrix.
 Use that line as a side of a square, draw one square above:
Use that line as a side of a square, draw one square above:
 and draw another square below:
and draw another square below:
 Finally sketch in the parabola with the vertex (
Finally sketch in the parabola with the vertex ( ,
, )
passing through corners of those two squares.
)
passing through corners of those two squares.
 Edwin
Edwin