Question 140955This question is from textbook college algebra
: Can I please get assistance with the following problem?
factor f(x) into linear factors given that k is a zero of f(x)
f(x)=x^3-6x^2-25x+150;k=5
THANK YOU!!
This question is from textbook college algebra
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since k=5 is a zero, this means that 5 is a test zero
So break down  by using synthetic division by using synthetic division
Set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the function to the right of the test zero.
Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 1)
Multiply 5 by 1 and place the product (which is 5) right underneath the second coefficient (which is -6)
Add 5 and -6 to get -1. Place the sum right underneath 5.
Multiply 5 by -1 and place the product (which is -5) right underneath the third coefficient (which is -25)
Add -5 and -25 to get -30. Place the sum right underneath -5.
Multiply 5 by -30 and place the product (which is -150) right underneath the fourth coefficient (which is 150)
| 5 | | | 1 | -6 | -25 | 150 | | | | | 5 | -5 | -150 | | | | 1 | -1 | -30 | |
Add -150 and 150 to get 0. Place the sum right underneath -150.
| 5 | | | 1 | -6 | -25 | 150 | | | | | 5 | -5 | -150 | | | | 1 | -1 | -30 | 0 |
Since the last column adds to zero, we have a remainder of zero. This means  is a factor of is a factor of 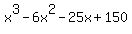
Now lets look at the bottom row of coefficients:
The first 3 coefficients (1,-1,-30) form the quotient
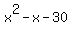
So 
You can use this online polynomial division calculator to check your work
Basically 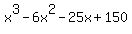 factors to factors to 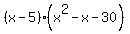
--------------------------------------------------------------------
Now lets break 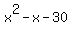 down further down further
Looking at 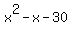 we can see that the first term is we can see that the first term is  and the last term is and the last term is  where the coefficients are 1 and -30 respectively. where the coefficients are 1 and -30 respectively.
Now multiply the first coefficient 1 and the last coefficient -30 to get -30. Now what two numbers multiply to -30 and add to the middle coefficient -1? Let's list all of the factors of -30:
Factors of -30:
1,2,3,5,6,10,15,30
-1,-2,-3,-5,-6,-10,-15,-30 ...List the negative factors as well. This will allow us to find all possible combinations
These factors pair up and multiply to -30
(1)*(-30)
(2)*(-15)
(3)*(-10)
(5)*(-6)
(-1)*(30)
(-2)*(15)
(-3)*(10)
(-5)*(6)
note: remember, the product of a negative and a positive number is a negative number
Now which of these pairs add to -1? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to -1
| First Number | Second Number | Sum | | 1 | -30 | 1+(-30)=-29 | | 2 | -15 | 2+(-15)=-13 | | 3 | -10 | 3+(-10)=-7 | | 5 | -6 | 5+(-6)=-1 | | -1 | 30 | -1+30=29 | | -2 | 15 | -2+15=13 | | -3 | 10 | -3+10=7 | | -5 | 6 | -5+6=1 |
From this list we can see that 5 and -6 add up to -1 and multiply to -30
Now looking at the expression 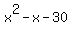 , replace , replace  with with 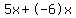 (notice (notice 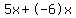 adds up to adds up to  . So it is equivalent to . So it is equivalent to  ) )
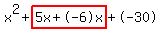
Now let's factor 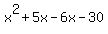 by grouping: by grouping:
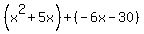 Group like terms Group like terms
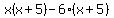 Factor out the GCF of Factor out the GCF of  out of the first group. Factor out the GCF of out of the first group. Factor out the GCF of  out of the second group out of the second group
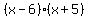 Since we have a common term of Since we have a common term of  , we can combine like terms , we can combine like terms
So 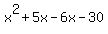 factors to factors to 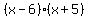 which means that which means that 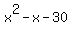 factors to factors to 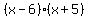
------------------------------------------------------------
Answer:
So 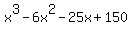 factors to factors to 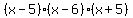
|
|
|