SOLUTION: Describe the pattern you observe in the table. Verify that the pattern continues by evaluating the four powers of i. i2= I need you to help me with the pattern all the way to

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: Describe the pattern you observe in the table. Verify that the pattern continues by evaluating the four powers of i. i2= I need you to help me with the pattern all the way to      Log On


   

Question 14019: Describe the pattern you observe in the table. Verify that the pattern continues by evaluating the four powers of i.
i2= I need you to help me with the pattern all the way to i40. Thanks. I
need it before 12:00p.m.
i3=
i4=
i5=
i6=
Found 2 solutions by Earlsdon, bam878s:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
First, remember that:
i+=+sqrt%28-1%29
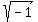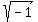If you square sqrt%28-1%29 you'll get -1.
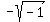So, i%5E2+=+-1 Now, if you multiply sqrt%28-1%29 by -1 you get:
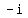
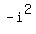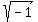
-sqrt%28-1%29 = -i and so it goes.
i+=+sqrt%28-1%29
i%5E2+=+%28sqrt%28-1%29%29%28sqrt%28-1%29%29 = %28sqrt%28-1%29%29%5E2+=+-1
i%5E3+=+%28i%5E2%29%28i%29 = %28-1%29%28sqrt%28-1%29%29+=+%28-1%29%28i%29 = -i
i%5E4+=+%28i%5E3%29%28i%29 = %28-i%29%28sqrt%28-1%29%29+=+%28-i%29%28i%29 = -i%5E2 = -%28-1%29+=+1
i%5E5+=+%28i%5E4%29%28i%29 = %281%29%28i%29+=+i = sqrt%28-1%29
and we start all over again.
See the pattern?
(i, i^2, i^3, i^4,), (i^5, i^6, i^6, i^7),(i^8, i^9, i^10, i^11)...
(i, -1, -i, 1), (i, -1, -i, 1), (i, -1. -i. 1)...

Answer by bam878s(77) About Me  (Show Source):
You can put this solution on YOUR website!
We know i=sqrt%28-1%29
so, i%5E2=-1.
i%5E3=i%5E2*i= -i.
i%5E4=i%5E2%2Ai%5E2 = 1.
i%5E5=i%5E2%2Ai%5E3 = i.
i%5E6=i%5E2%2Ai%5E4= -1 * 1 = -1.
i%5E7=i%5E4%2Ai%5E3= 1 * -i = -i.
i%5E8=i%5E4%2Ai%5E4= 1 * 1 = 1.
i%5E9=i%5E3%2Ai%5E6 = -i * -1 = i.
It follows that it follows this pattern throughout from here.
Note, I made use of this formula x%5En%2Ax%5Em=x%5E%28n%2Bm%29.
Hope this helps.