|
Question 139744: What is the graph, vertex and intercepts of: y= x^2+3x-1
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! You have an equation in the form  , where your coefficient values are  ,  , and  .
First find the vertex:
The x-coordinate of the vertex is given by 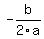 . Just substitute the values and calculate.
The y-coordinate of the vertex is the value of the function at the x-coordinate of the vertex. So just substitute the value of the x-coordinate you just calculated into the function everywhere you see an x, and do the arithmetic.
Start your graph. Plot the vertex.
Next find the y-intercept. This is the place that the curve crosses the y-axis, or where x = 0. You will get y=c, or y=-1 in this case, so your y-intercept is (0,-1) Plot that point.
Next find the x-intercepts. These are the points where the curve crosses the x-axis, or the points where the value of the function is 0. Set your expression equal to 0 and solve the quadratic equation. Since this beast doesn't factor neatly, you have two choices: Either complete the square, or use the quadratic formula. You are going to get two real number values with this one, and I know this because the value of the quadratic discriminant is positive, so let's say they are r and s. That means your x-intercepts are (r,0) and (s,0). Of course, you have to figure out what values to substitute for r and s. Plot these points.
You can find one additional point easily. Because the curve is symmetrical, there is a point with a y-coordinate equal to the y-coordinate of the y-intercept at an x-coordinate 2 times the value of the vertex x-coordinate. Plot that point.
All of that gives you five points to plot. Draw a smooth curve through these points remembering that this is a parabola and that it opens upward because the lead coefficient (the  in ) is positive.
|
|
|
| |
