Question 139591This question is from textbook Algebra Structure and Method
: I have been struggling with this problem and I was wondering if anyone could help me? I would deeply appreciate it! Please and Thank you!
Factoring Patterns for ax^2+bx+c
Factor. Check by multiplying the factors. If the polynomial is not factorable, write prime.
2(x-y)^2-9(x-y)z-5z^2
This question is from textbook Algebra Structure and Method
Found 2 solutions by jim_thompson5910, solver91311:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 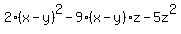 Start with the given equation Start with the given equation
Let 
 Plug in Plug in 
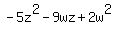 Sort the terms in descending order Sort the terms in descending order
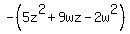 Factor out a negative one Factor out a negative one
Now let's factor the inner polynomial 
Looking at  we can see that the first term is we can see that the first term is 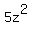 and the last term is and the last term is 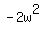 where the coefficients are 5 and -2 respectively. where the coefficients are 5 and -2 respectively.
Now multiply the first coefficient 5 and the last coefficient -2 to get -10. Now what two numbers multiply to -10 and add to the middle coefficient 9? Let's list all of the factors of -10:
Factors of -10:
1,2,5,10
-1,-2,-5,-10 ...List the negative factors as well. This will allow us to find all possible combinations
These factors pair up and multiply to -10
(1)*(-10)
(2)*(-5)
(-1)*(10)
(-2)*(5)
note: remember, the product of a negative and a positive number is a negative number
Now which of these pairs add to 9? Lets make a table of all of the pairs of factors we multiplied and see which two numbers add to 9
| First Number | Second Number | Sum | | 1 | -10 | 1+(-10)=-9 | | 2 | -5 | 2+(-5)=-3 | | -1 | 10 | -1+10=9 | | -2 | 5 | -2+5=3 |
From this list we can see that -1 and 10 add up to 9 and multiply to -10
Now looking at the expression  , replace , replace  with with  (notice (notice  adds up to adds up to  . So it is equivalent to . So it is equivalent to  ) )

Now let's factor 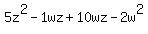 by grouping: by grouping:
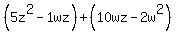 Group like terms Group like terms
 Factor out the GCF of Factor out the GCF of  out of the first group. Factor out the GCF of out of the first group. Factor out the GCF of 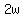 out of the second group out of the second group
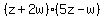 Since we have a common term of Since we have a common term of 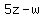 , we can combine like terms , we can combine like terms
So 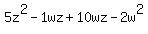 factors to factors to 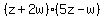
So  factors to factors to 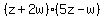
This means that 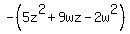 factors to factors to 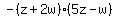 (remember, we pulled out a negative one previously) (remember, we pulled out a negative one previously)
 Now replace "w" with Now replace "w" with 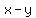
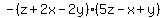 Distribute Distribute
-------------------------------
Answer:
So 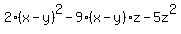 factors to factors to 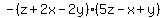
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is a slight flaw in your terminology. ALL 2nd degree trinomials can be expressed as the product of two factors,  and and 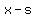 . The thing is, r and s aren't always integers or even rational numbers. I suspect your instructor meant to say "If the polynomial is not factorable over the integers (or rationals), write prime." . The thing is, r and s aren't always integers or even rational numbers. I suspect your instructor meant to say "If the polynomial is not factorable over the integers (or rationals), write prime."
With this ungodly horror, 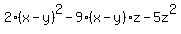 , recognize that the independent variable is , recognize that the independent variable is 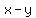 , so let's clean it up a bit by saying , so let's clean it up a bit by saying  . That let's us rewrite the expression: . That let's us rewrite the expression: 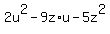 . Now we can see that the pattern . Now we can see that the pattern  means that means that  , ,  , and , and 
Now we can use the fact that  and and  are roots of are roots of  if and only if if and only if  and and 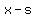 are factors of are factors of 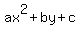 . .
So let's find the roots of  using the quadratic formula: using the quadratic formula:




 or or 
 or or 
 or or 
That means that either  or or  (which is equivalent to (which is equivalent to  . .
Hence our factors so far are  , but remember that , but remember that  , so: , so:
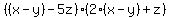 are your two factors. are your two factors.
|
|
|