|
Question 139251: i have tried so hard to figure out this problem but it seems so difficult.
Given the function f(x)=2x^2-8x+3, answer the following questions using specific language to explain each step performed.
1.)determine the nature of the roots, using the discriminant.
2.) solve by using the quadratic formula
3.) graph using vertex roots and direction
4,)what is the minimum? maximum?
5.) what is the axis of symmetry?
how do i show all of this?
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the function f(x)=2x^2-8x+3, answer the following questions using specific language to explain each step performed.
----------------------------
1.)determine the nature of the roots, using the discriminant.
discriminant = b^2-4ac
d = 8^2-4*2*3 = 64 - 24 = 40 > 0
Since d>0, the function has two unequal Rean Number solutions.
----------------------------------------
2.) solve by using the quadratic formula
x = [8 +- sqrt(40)]/4
x = 2 +- (1/2)sqrt(10)
-------------------------------
3.) graph using vertex roots and direction
Vertex occurs at x=-b/2a = 8/4 = 2
f(2) = 8-16+3 = -5
Vertex: (2,-5)
Direction:Since the coefficient of x^2 is positive, the parabola opens up.

------------------------
4,)what is the minimum?
y=-5
maximum?
There is no maximum as the parabola opens up.
---------------------------
5.) what is the axis of symmetry?
The vertical line thru the vertex: x=2
=========================================
Cheers,
Stan H.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! The quadratic formula is  . The discriminant is that part of the quadratic formula under the radical sign, specifically: . The discriminant is that part of the quadratic formula under the radical sign, specifically:  . .
if the discriminant is positive, then there are two different real roots.
if the discriminant is zero, then there are two identical real roots (or one real root with a multiplicity of two -- depends on the language your instructor likes).
if the discriminant is negative, then the roots are a conjugate pair of complex roots of the form 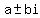 where where  is the imaginary number defined by is the imaginary number defined by  . .
For your equation,  , ,  , and , and  , so just substitute those values into the quadratic formula shown above and do the arithmetic. , so just substitute those values into the quadratic formula shown above and do the arithmetic.
To graph:
Find the vertex. The x-coordinate of the vertex is actually the numerical average of the two roots (that's because of symmetry), or 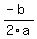 . Just calculate it. The y-coordinate of the vertex is the value of the function at the x-coordinate, or . Just calculate it. The y-coordinate of the vertex is the value of the function at the x-coordinate, or 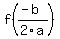 . Plot the point. . Plot the point.
You already have the roots from an earlier step, so if they are r and s, plot the points, (r,0) and (s,0) (you will have to approximate the square root of 10 - that's a hint, by the way).
The direction of a parabola is determined by the sign on the lead coefficient. Positive (like this one) opens up, negative opens down.
You can also easily compute the y-intercept, or where the curve crosses the y-axis by substituting 0 for x. You will get y = the value of the constant term, 3 in this case, so the y-intercept is (0,3).
Also, because of symmetry, there is a point at ( ,3). ,3).
Plot all of these points and draw a smooth curve.
Since this is a parabola that opens upward, the value of the function (i.e. the y-coordinate) at the vertex is the minimum, and there is no maximum.
The axis of symmetry is the vertical line that passes through the vertex. The equation is  . .
All you need to do now is a little arithmetic and plot your graph.
|
|
|
| |