Question 138682: Graph 
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Start with the given function Start with the given function
Looking at the numerator  , we can see that the degree is , we can see that the degree is  since the highest exponent of the numerator is since the highest exponent of the numerator is  . For the denominator . For the denominator 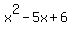 , we can see that the degree is , we can see that the degree is  since the highest exponent of the denominator is since the highest exponent of the denominator is  . .
Horizontal Asymptote:
Since the degree of the numerator (which is  ) is less than the degree of the denominator (which is ) is less than the degree of the denominator (which is  ), the horizontal asymptote is always ), the horizontal asymptote is always 
So the horizontal asymptote is 
--------------------------------------------------
Vertical Asymptote:
To find the vertical asymptote, just set the denominator equal to zero and solve for x
 Set the denominator equal to zero Set the denominator equal to zero
Now let's use the quadratic formula to solve for x. If you need help with the quadratic formula, check out this solver.
After using the quadratic formula, we get the solutions
 or or 
So this means the vertical asymptotes are  or or 
--------------------------------------------------
X-Intercept(s)
 Start with the given function Start with the given function
 Plug in Plug in 
 Solve for x Solve for x
So the x-intercept is (0,0). Since there can only be one y-intercept, the y-intercept is also (0,0)
Now let's use this info to graph  : :
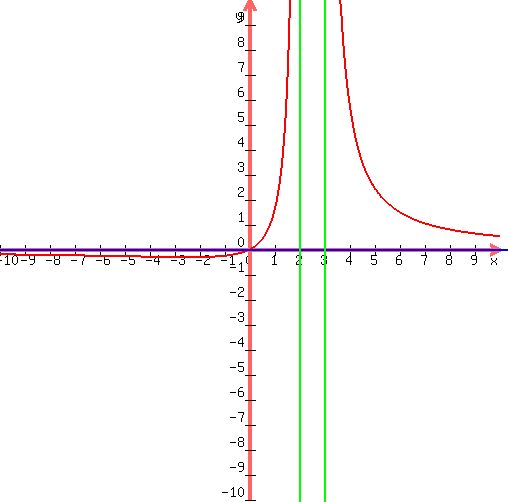 Graph of Graph of  with the horizontal asymptote with the horizontal asymptote  (blue line) , the vertical asymptotes (blue line) , the vertical asymptotes  and and  (green lines), and the x and y intercept (0,0) (green lines), and the x and y intercept (0,0)
|
|
|