|
Question 137634This question is from textbook College Algebra Fifth Ed.
: Finding (f*g)(x) and (g*f)(x) and the domain of the following.
f(X)= squared root of x+1
g(x)= squared root of x-1
This question is from textbook College Algebra Fifth Ed.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your terminology is a bit odd, so I'm a little confused as to whether you mean  or or  . I'll presume the former and you can write back if that isn't correct. . I'll presume the former and you can write back if that isn't correct.


If you are given a function f, then f(x) means "the value of the function at f"
So if  , ,  , ,  , , 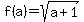 . (f°g)(x) is nothing more than . (f°g)(x) is nothing more than  , so (f°g)(x)= , so (f°g)(x)= 
To find the domain of (f°g)(x), first find the domain of g. The value under the radical cannot be negative, so  must be non-negative, in other words must be non-negative, in other words  , or , or  . Which is to say that anything less than 1 must be excluded. . Which is to say that anything less than 1 must be excluded.
Now let's examine the domain of f. Using similar analysis, the domain of f is 
So for the composite function, we have to restrict g(x) to be greater than -1.
In other words,  . .
Since g(x) is positive for all values of x in the domain of g, g(x) is also greater than or equal to -1 for all values of x in the domain of g.
Hence, the only restriction on (f°g)(x) is that  , and therefore the domain of (f°g)(x) is the interval [1, , and therefore the domain of (f°g)(x) is the interval [1, ) )
You should be able to handle the other part of this problem now.
|
|
|
| |