Question 137613: Can 4u^2-9u+4 be factored? If so could you please show me how?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Well, the answer to your first question is yes and no. In fact, all quadratic polynomials can be factored, but the question becomes what is the nature of those factors. In fact, given 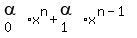 +...+ +...+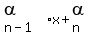 , , is a factor if and only if is a factor if and only if  is a root of is a root of 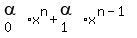 +...+ +...+ . .
So all you need to do is find the two roots of  , let's say they are , let's say they are  and and  , then your factors of , then your factors of 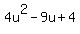 are are 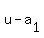 and and 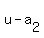 . .
On the other hand, I think you meant to ask if 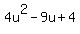 is factorable over the integers or perhaps the rationals. If that is what you meant, then the answer is most certainly no. That is because the roots of is factorable over the integers or perhaps the rationals. If that is what you meant, then the answer is most certainly no. That is because the roots of  are irrational, specifically are irrational, specifically  and and  a conjugate pair of irrational numbers. a conjugate pair of irrational numbers.
|
|
|