Question 137056: Is there a short way to do the SUM of a sequence of sums: (1) + (1+2) + (1+2+3) + (1+2+3+4) + .... (1+2+3+4....+100). I know how to do the sum of the sequence (i.e. sum of 100= 100/2(100 + 1)) and I can get the answer, I am just trying to see if there is an easier way then adding each number up. Like, sum for 100 is 5050; sum of 99 is sum of 100 minus 100 or 4050; but I can't find a shortcut and I can't find a formula anywhere for the sum of a series of sums. Can someone help? This is actually not for a class.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given: The first term of every summation in the series is  . .
Given: The number of numbers in each summation is 1 greater than the previous term.
Given: There are  terms in the series. terms in the series.
The first term of your series must be 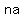 , because every term in the series will have an , because every term in the series will have an  in it. in it.
The second term of your series must be 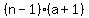 , because all but the first term will have an , because all but the first term will have an 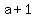 in it. This expands to: in it. This expands to: 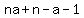
The third term of your series must be 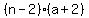 , similar logic, and this expands to , similar logic, and this expands to 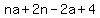
This gives us the idea that the i-th term must be 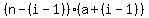 , which expands to , which expands to 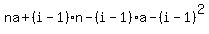
Notice that every term has an 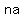 term, so there must be term, so there must be  times times 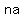 in your sum. The first term of the shortcut formula is then in your sum. The first term of the shortcut formula is then 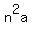
If you sum all of then  terms, you find that the coefficients can be expressed as terms, you find that the coefficients can be expressed as  . Since . Since  , ,  . Hence, the second term of the shortcut formula must be . Hence, the second term of the shortcut formula must be 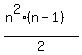 . .
Similarly, the sum of all the  terms must be terms must be 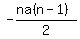 . .
Finally, the last term is  because the sum of squares is because the sum of squares is  . .
Putting it all together:

I won't go into the details of the derivation, but if you have a common difference other than 1, call it  , the formula becomes: , the formula becomes:

|
|
|