SOLUTION: I have the following problem. It has exponents so I will try to explain where they are. Complex Fraction: Numerator: x to exponent -3 plus y to exponent -5 Denominator: x to

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: I have the following problem. It has exponents so I will try to explain where they are. Complex Fraction: Numerator: x to exponent -3 plus y to exponent -5 Denominator: x to       Log On


   

Question 136998: I have the following problem. It has exponents so I will try to explain where they are.
Complex Fraction:
Numerator: x to exponent -3 plus y to exponent -5
Denominator: x to exponent -2 plus y to exponent -4

I know that you cannot have negative exponents so they have to be changed to fractions within the larger fraction:
Numerator: 1 over x to exponent 3 plus 1 over y to exponent 5
Denominator: 1 over x to exponent 2 plus 1 over y to exponent 4
This is where I get stuck. I know that dividing fractions means taking the first fraction times the reciprical of the second fraction. But the computer program (I am using Coursecompass.com for my math class) wants me to find a common denominator??? Im confused why I need a common denominator, how to find it, and what to do with it.
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
You were given:

%28x%5E%28-3%29%2By%5E%28-5%29%29%2F%28x%5E%28-2%29%2By%5E%28-4%29%29

And you changed it to:

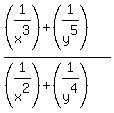
%28%281%2Fx%5E3%29%2B%281%2Fy%5E5%29%29%2F%28%281%2Fx%5E2%29%2B%281%2Fy%5E4%29%29

So far, so good. Finding the LCD for rational expressions using variables is no different from finding the LCD for regular fractions that just involve numbers. You remove any common factors and then multiply the factors that remain. If there aren't any common factors, you just multiply the two numbers. Here's a couple of examples using just numbers:

1%2F2%2B1%2F6. The factorization of 2 is just 2, and the factorization of 6 is 2 * 3. You need one factor of 2 and one factor of 3 to account for all of the factors in the two numbers without duplication, so the LCD is just 2 * 3 = 6, and the sum works out to %281%2F2%29%283%2F3%29%2B%281%2F6%29=3%2F6%2B1%2F6=4%2F6.

On the other hand, if you had something like 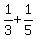1%2F3+%2B+1%2F5, there are no common factors between 3 and 5, so the LCD is just 3 * 5 = 15. That means the sum becomes: %281%2F3%29%285%2F5%29%2B%281%2F5%29%283%2F3%29=5%2F15%2B3%2F15=8%2F15.

YOu proceed in the same fashion with denominators that contain variables. There are no common factors between x%5E3 and y%5E5, so the LCD is just the product of the two or x%5E3y%5E5

So the numerator of your big fraction becomes:

I'll let you apply the process to your denominator. Once you have the denominator done, remember to invert the denominator and multiply. Also, remember that x%5Em%2Fx%5En=x%5E%28m-n%29