Question 136358: A nationwide test taken by high school sophomores and juniors has three sections, each scored on a scale of 20 to 80. In a recent year, the national mean score for the writing section was 51.2. Based on this information, complete the folloiwng staements about the distribution of the scores on the writing section for the recent year.
1. According to Chebyshev's theorem, at least ____% fo the scores lie within 2.5 standard deviations of the mean, 51.2.
2. Suppose that the distribution is bell shaped. If approximately 99.7% of the scores lie between 23.6 and 78.8, then the approximate value of the standard deviation for the distribution, according to the empirical rule, is _____?
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! A nationwide test taken by high school sophomores and juniors has three
sections, each scored on a scale of 20 to 80. In a recent year, the national
mean score for the writing section was 51.2. Based on this information,
complete the folloiwng staements about the distribution of the scores on the
writing section for the recent year.
1. According to Chebyshev's theorem, at least ____% fo the scores lie within
2.5 standard deviations of the mean, 51.2.
Chebyshev's theorem states:
At least 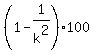 % of any set of data will lie within k standard
deviations of the mean (where % of any set of data will lie within k standard
deviations of the mean (where 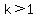 )
Your problem has k = 2.5, so we substitute in Chebyschev's theorem:
At least )
Your problem has k = 2.5, so we substitute in Chebyschev's theorem:
At least 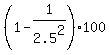 % of any set of data will lie within 2.5 standard
deviations of the mean (where % of any set of data will lie within 2.5 standard
deviations of the mean (where 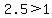 )
At least )
At least 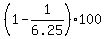 % of any set of data will lie within 2.5 standard
deviations of the mean (where % of any set of data will lie within 2.5 standard
deviations of the mean (where  )
At least )
At least 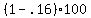 % of any set of data will lie within 2.5 standard
deviations of the mean (where % of any set of data will lie within 2.5 standard
deviations of the mean (where  )
At least )
At least 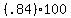 % of any set of data will lie within 2.5 standard
deviations of the mean (where % of any set of data will lie within 2.5 standard
deviations of the mean (where 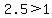 )
At least )
At least  % of any set of data will lie within 2.5 standard deviations
of the mean (where % of any set of data will lie within 2.5 standard deviations
of the mean (where 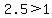 )
------------------ )
------------------
2. Suppose that the distribution is bell shaped. If approximately 99.7% of the
scores lie between 23.6 and 78.8, then the approximate value of the standard
deviation for the distribution, according to the empirical rule, is _____?
The empirical rule is in three parts:
If a distribution is roughly bell shaped, then
1. Approximately 68% of the data will lie within 1 standard deviation of the
mean. That is approximately 68% of the data lie between 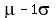 and and
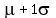 .
2. Approximately 95% of the data will lie within 2 standard deviation of the
mean. That is approximately 95% of the data lie between .
2. Approximately 95% of the data will lie within 2 standard deviation of the
mean. That is approximately 95% of the data lie between 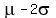 and and
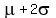 .
3. Approximately 99.7% of the data will lie within 3 standard deviation of the
mean. That is approximately 99.7% of the data lie between .
3. Approximately 99.7% of the data will lie within 3 standard deviation of the
mean. That is approximately 99.7% of the data lie between 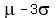 and and
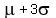 .
Since 99.7% is given, we only need the 3rd statement above.
Now to make sure we can use that 3rd statement, we must first confirm that .
Since 99.7% is given, we only need the 3rd statement above.
Now to make sure we can use that 3rd statement, we must first confirm that
 , which equals 51.2 is halfway between the two values 23.6 and 78.8.
We do that by averaging them and seeing if we get the mean 51.2. , which equals 51.2 is halfway between the two values 23.6 and 78.8.
We do that by averaging them and seeing if we get the mean 51.2.
 Yes we do, so now we know that
Yes we do, so now we know that  and and  are both the same distance from the mean
are both the same distance from the mean  .
Substituting .
Substituting  in either in either
 or or 
 or or  Solving the first gives:
Solving the first gives:
 add
add 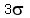 to both sides: to both sides:
 Subtract 23.6 from both sides gives:
Subtract 23.6 from both sides gives:
 Divide both sides by 3
Divide both sides by 3

 --------------------------------------------
Solving the second (only as a check) gives:
--------------------------------------------
Solving the second (only as a check) gives:
 add
add 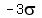 to both sides: to both sides:
 Subtract 78.8 from both sides gives:
Subtract 78.8 from both sides gives:
 Divide both sides by -3
Divide both sides by -3

 That's the standard deviation.
Edwin
That's the standard deviation.
Edwin
|
|
|