|
Question 136225: I need to figure out how to set these up. Thank you
You can use 1 mile = 5,280 feet for your conversions
1.Many people know that the weight of an object varies on different planets, but did you know that the weight of an object on earth also varies according to the elevation of the object? In particular, the weight of an object follows this equation: w=Cr^-2 , where C is a constant, and r is the distance that the object is from the center of the earth.
a.Solve the equation w=Cr^-2 for r.
b.Suppose that an object is 100 pounds when it is at sea level. Find the value of C that makes the equation true. (Sea level is 3,963 miles from the center of the earth.)
c.Use the value of C you found in the previous question to determine how much the object would weigh in
i. Death Valley (282 feet below sea level)
ii. The top of Mt McKinley (20,430 feet above sea level)
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! a. Solve  for  . Remember  , so  . Multiply both sides by  , divide both sides by  , then take the positive square root of both sides.
b. You first need to solve for C. Use what we discovered in part a.  . Multiply both sides by C. Substitute 100 for w and 3963 for r and do the arithmetic. The result will be the value for C.
c.i. The radius of the earth is given in miles, and you calculated C on that basis, so you need to convert the difference between Death Valley's elevation and sea level, 282 feet into miles,  , and then subtract this value from 3963. This is your new value for r. Using the value for C from part b and this new value for r, use the original formula to calculate the weight in Death Valley.
c.ii. Same process, except that you need to calculate 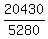 and add that result to 3963 to get your radius.
|
|
|
| |
