Question 136110: What is the difference between domain and range? Describe a real life situation that could be modeled by a function
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! if f is a function, f(x) is the value of the function at x. The domain of the function is the set of all possible values for which the function is defined.
For example (note that the following presumes that the functions are mapped to the real numbers):
 . f is defined for all real values of x. Hence the domain is all reals. . f is defined for all real values of x. Hence the domain is all reals.
 . if . if  , then the denominator is zero, so g is not defined for , then the denominator is zero, so g is not defined for  , therefore the domain is the set of all x such that x is a real number and x is not equal to 2. , therefore the domain is the set of all x such that x is a real number and x is not equal to 2.
 . if . if 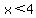 then the quantity under the radical is negative, meaning h is not defined in the reals. Therefore the domain of the function is the set of all x such that x is real and then the quantity under the radical is negative, meaning h is not defined in the reals. Therefore the domain of the function is the set of all x such that x is real and  . .
The range is the set of all possible values of the function over the domain of the function.
Using the above examples:
 . This function is continuous over the reals and as x increases without bound, f(x) increases without bound. The range is all reals. . This function is continuous over the reals and as x increases without bound, f(x) increases without bound. The range is all reals.
 . For any real value of x, . For any real value of x,  , g(x) maps to a real number, and for any value of g(x), an x exists that will map to that g(x). The range is all reals. , g(x) maps to a real number, and for any value of g(x), an x exists that will map to that g(x). The range is all reals.
 . The notational convention is that the radical means the positive square root. If it were taken to mean either the positive or negative square root, h would not be a function because for all values of x in the domain of h except . The notational convention is that the radical means the positive square root. If it were taken to mean either the positive or negative square root, h would not be a function because for all values of x in the domain of h except  , h(x) could take on two different values, thus violating the definition of a function. Therefore, the range of this function is all non-negative reals (all positive reals and zero). Expressed as a set: the set of all y such that y is real and , h(x) could take on two different values, thus violating the definition of a function. Therefore, the range of this function is all non-negative reals (all positive reals and zero). Expressed as a set: the set of all y such that y is real and  . .
 where where  is the number of gallons of capacity in your automobile gas tank and is the number of gallons of capacity in your automobile gas tank and  is the cost per gallon at the pump. The function results in the total cost for a tank of gasoline. is the cost per gallon at the pump. The function results in the total cost for a tank of gasoline.
|
|
|