Question 135973: Q. Show that 2 - i is a root of z^4 - 8z^3 + 28z^2 - 48z + 35. Hence fond all the roots
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Actually, technically speaking, and we should always speak technically when talking about this stuff, 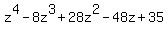 doesn't have any roots. doesn't have any roots.  has roots, and those roots are related to the factors of has roots, and those roots are related to the factors of 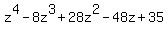 as we shall see shortly. as we shall see shortly.
Assume that 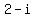 is a root of is a root of 
Then 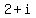 must also be a root of must also be a root of  because complex roots always occur in conjugate pairs. because complex roots always occur in conjugate pairs.
 is a root of a polynomial equation if and only if is a root of a polynomial equation if and only if  is a factor of the polynomial. That means that both is a factor of the polynomial. That means that both 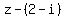 and and  are factors of are factors of 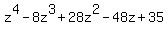 . Furthermore, the product of those two factors must also be a factor of . Furthermore, the product of those two factors must also be a factor of 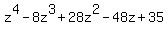 . .
The product of 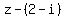 and and  , ,  works out to works out to  (recalling that (recalling that  so so  ) )
Since 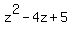 is a factor of is a factor of 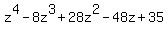 , the result of polynomial long division of , the result of polynomial long division of 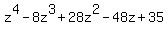 by by 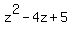 will be a quotient polynomial with a zero remainder. If this is true, then our original assumption is true, i.e., will be a quotient polynomial with a zero remainder. If this is true, then our original assumption is true, i.e., 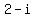 is a root of is a root of  because we will have proven that because we will have proven that 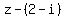 is a factor of is a factor of 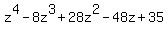
===============================================================
Polynomial Long Division Process
===============================================================
 goes into goes into   times. times. 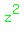 is the first term of the quotient. is the first term of the quotient.
Multiply  times times 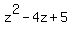 to get to get 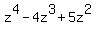 and subtract from and subtract from 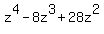 resulting in resulting in 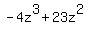 . Bring down the . Bring down the 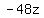 to form to form 
 goes into goes into 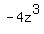 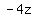 times. times. 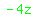 is the second term of the quotient. is the second term of the quotient.
Multiply 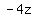 times times 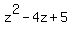 to get to get  and subtract from and subtract from  resulting in resulting in 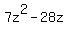 . Bring down the . Bring down the  to form to form 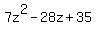
 goes into goes into 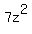  times. times.  is the third term of the quotient. is the third term of the quotient.
Multiply  times times 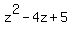 to get to get 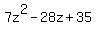 and subtract from and subtract from 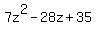 resulting in a remainder of zero. The quotient is the sum of the three parts noted above, namely resulting in a remainder of zero. The quotient is the sum of the three parts noted above, namely 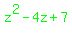
===============================================================
End of Polynomial Long Division Process
===============================================================
That means that 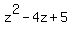 is a factor of is a factor of 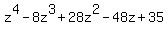 , and therefore , and therefore 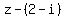 must also be a factor of must also be a factor of 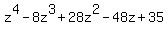 , and finally , and finally  (and its conjugate, (and its conjugate,  )must be a root of )must be a root of  . .
Since  is a quartic (degree 4) polynomial equation, there must be 4 roots. We have found two of them. Since the quotient derived by the polynomial long division process just performed must also be a factor of is a quartic (degree 4) polynomial equation, there must be 4 roots. We have found two of them. Since the quotient derived by the polynomial long division process just performed must also be a factor of 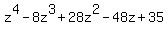 , the factors of that quotient must also be factors of , the factors of that quotient must also be factors of 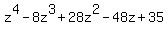 . .
Therefore solving  will give the remaining two roots of will give the remaining two roots of  . I'll leave that one to you. Hint: The quadratic does NOT factor over the integers (or the reals, for that matter), so either complete the square or use the quadratic formula. I completed the square and that worked out rather tidily. Write back and tell me your results. . I'll leave that one to you. Hint: The quadratic does NOT factor over the integers (or the reals, for that matter), so either complete the square or use the quadratic formula. I completed the square and that worked out rather tidily. Write back and tell me your results.
The following graph of  supports the notion that there are no real roots to your given equation because the graph does not intersect the x-axis, so supports the notion that there are no real roots to your given equation because the graph does not intersect the x-axis, so 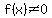 for all real x. for all real x.

|
|
|