Question 135897: I am asked to find the surface area and volume a 3D composite solid. It has a pyramid on the top and a square-based cylinder on the bottom. The slant height of the pyramid is 5m, the height of the square-based prism is 8m and the square has equal sides measuring 6m. I have tried figuring out the surface area of the pyramid, using the formula S.A. = 1/2Ps + B., and adding this to the surface area of the square-based prism, using S.A.= Ph + 2B. P is the perimeter of the base, s is the slant height and B is the area of the base. H is the height of the perpendicular distance between the two bases. Could you please help me with this question. Thank you in advance.
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!  is the correct formula for the surface area of a pyramid where  is the area of the base, p is the perimeter of the base, and s is the slant height along a bisector of a face (measured from the midpoint of any edge to the apex of the pyramid). However, you have a pyramid that is part of a complex solid with the base of the pyramid mated to one base of the square based prism. Therefore the area of the base should not be included in the calculation of the surface area of the pyramid part of the solid. Hence,  . Since the pyramid has a base that matches the square base of the square based prism, each edge of the pyramid base measures 6m. So the perimeter of the base is  . Putting it together 
 is the formula for the surface area of a prism where B is the area of the base, p is the perimeter of the base and h is the height of the prism. But again, you have to eliminate the area of one of the bases because one of them mates to the bottom of the pyramid. So the applicable formula is:  . The area of the base is simply the area of a 6 by 6 square, or 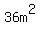 , and the perimeter of the base is the same as that for the pyramid, namely 24m. So:
Adding the two surface areas together, 
The volume of a pyramid is given by  where B is the area of the base and h is the height of the pyramid which is the measure of a segment perpendicular to the base through the apex. We are given the slant height, but the slant height and one-half of the base edge measure forms a right triangle with the height, the slant height being the hypotenuse. Therefore, the height of the pyramid is  . The area of the pyramid base is the same as the area of the prism base, namely 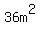, so the volume of the pyramid is 
The volume of a prism is given by  where B is the area of the base and h is the height. We already know the area of the base and we are given the height, so: 
Together 
|
|
|
