Question 135617: Write a quadratic equation for which the following are solutions for x: ± 3i
This one has me a bit confused. Here's what I get
x = ±i sqrt 9
x = ± sqrt -9
x^2=-9
x^2+9=0
That's not a complete quadratic equaiton, but I don't know what to do next or if I'm doing it right to begin with.
Found 2 solutions by Earlsdon, solver91311:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! You sort of took a convoluted path to get there, but you did arrive at the right answer.
Here's how I would have done it:
A polynomial equation has a root  if and only if if and only if  is a factor of the polynomial. Furthermore, a polynomial equation of degree n has exactly n roots. is a factor of the polynomial. Furthermore, a polynomial equation of degree n has exactly n roots.
You are given two roots, so you know that you must have a quadratic (degree 2) polynomial equation.
The roots are 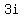 and and 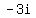 , therefore, the factors of the polynomial must be , therefore, the factors of the polynomial must be  and and  . .
Multiply the two factors together:  (factorization of the difference of two squares in reverse) (factorization of the difference of two squares in reverse)
So your equation is  . .
And, by the way, it most certainly is a 'complete' quadratic equation of the form  : :  , ,  , and , and  . The only restriction on the possible values for the coefficients in . The only restriction on the possible values for the coefficients in  is that is that 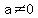 . b and c can be any values, including zero. . b and c can be any values, including zero.
|
|
|