Question 135278: Please help me with this equation-Thank You!
Find a polynomial equation with real coefficients that has the given roots.
3, -9, 3+2i
Found 2 solutions by scott8148, solver91311:
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! if r is a root, then x-r is a factor
complex roots (3+2i) occur in conjugate pairs, so 3-2i is also a root
(x-3)(x+9)(x-3-2i)(x-3+2i)=0
multiply the factors to find the equation
__ HINT: start with the complex factors, it will be less "messy"
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two things:
First, if a polynomial equation has a complex number root ( ), then it also has the conjugate of that complex number as a root ( ), then it also has the conjugate of that complex number as a root (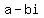 ). That means that, although you were only given three numbers as roots, there are actually four, namely: ). That means that, although you were only given three numbers as roots, there are actually four, namely:
 , ,  , , 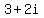 , and , and 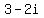
Second, a polynomial equation has a root  if and only if if and only if 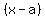 is a factor of the polynomial. is a factor of the polynomial.
So if the desired polynomial is  , then , then  . All you need to do now is multiply the factors and collect like terms. Hint: Remember when you are working it out that . All you need to do now is multiply the factors and collect like terms. Hint: Remember when you are working it out that  , so , so  not not  . .
|
|
|