Question 135217: A coin was flipped 60 times and came up heads 38 times. (a) at the .10 level of significance, is the coin biased toward heards? Show your decision rule and calculations. (b) Calculate a p-value and interpret it.
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! A coin was flipped 60 times and came up heads 38 times.
p-hat = 38/60 = 19/30
-------------------------
(a) at the .10 level of significance, is the coin biased toward heads? Show your decision rule and calculations.
Ho: p= 1/2
Ha: p> 1/2
------------
Critical value of one-tail z-test with alpha = 5%: z = 1.645
-------------
Test statistic: z(19/30) = ((19/30)-(1/2))/sqrt[(0.5*0.5)/60] = 0.1333/0.0645
= 2.0651
----------
Conclusion: Since test stat lies in the rejection interval, Reject Ho.
The test provides statistical evidence the coin is biased toward heads.
-------------
(b) Calculate a p-value and interpret it.
p-value = P(2.0651 < z < 10) = 0.0191
That means there is only a 1.91% chance the statistical results could
have provided stronger evidence for rejecting Ho.
=============================
Cheers,
Stan H.
------------------
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website! Stanbon's solution is incorrect. He divided alpha .10 by 2, getting .05, which should only have been done if the test had been two-tailed, but this is a right-tail test.
A coin was flipped 60 times and came up heads 38 times. (a) at the .10 level of significance, is the coin biased toward heads? Show your decision rule and calculations.
H0: p = 
Ha: p >
This is a one-tail (right-tail) test
z =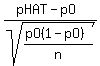 
where  =  =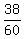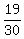 
 = 
z = 
z =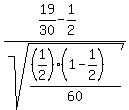 
z = 
z = 
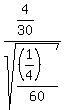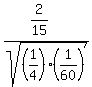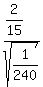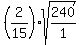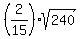z =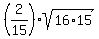 
z = 
z =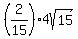 
z = 
z =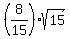 
z = 
z =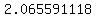 
The .10 level of significance means that
we will reject the null hypothesis if 2.065591118
is greater than the z-value which has .10 (10%) of
area under the standard normal curve to the right
of it.
Now there are two kinds of normal tables in use today,
and I don't know which you have.
If you have the kind that accumulates the area to the
right of z=0, then subtract .5-.10 = .40, then look
through the body of the table and find the nearest
value to .4000, which is .3997, and observe that that
occurs at z = 1.28.
If you have the kind that accumulates the area from
the extreme left, then subtract 1-.10 = .90, then look
through the body of the table and find the nearest
value to .9000, which is .8997, and observe that that
occurs at z = 1.28.
Since our z-value of 2.065591118 is to the right of
1.28, then we reject the null hypothesis and conclude
that the probability of heads is greater than ,
thus it is biased toward heads.
(b) Calculate a p-value and interpret it.
This is different way of completing the problem. Instead
of finding the value of z which has .10 (10%) of the
area to the right of it, we find instead the area to the
right of the z value which we have calculated above, and
then reject the null hypothesis only if that area is less
than .10.
So we find the area to the right of
z = 2.065591118
So regardless of which table you have, look up the nearest
value of z to that, which is 2.07.
If you have the kind of table that accumulates area from
z = 0, then you will read .4808, then subtract that from
.5000 to get the p-vale as .0192.
If you have the kind of table that accumulates area from
the extreme left, then you will read .9808, then subtract
that from 1.0000 to get the p-value as .0192.
Since this p-value is less than .10, our z-score has less
than .10, and we therefore reject the null hypothesis, and
thus we conclude that the coin is biased toward heads.
To interpret the p-value for this problem:
If the coin were not biased, then the probability of getting
38 or more heads out of 60 would be only .0192.
Edwin
|
|
|
