Question 135205: calculate the value of the discriminant of x^ + 2x +1 = 0 by examining the sign of the discriminant in part a, how many x- intercepts would the graph of y + x^ + 2x +1 have ? Why?
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! The discriminant of  is 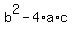 . For your equation, a = 1, b = 2, and c =1.
If the discriminant is >0 (positive), then there are two different real roots to the equation. Graphically this means that the graph of the function  will intersect the x axis in two different points.
If the discriminant = 0, then there are two real and identical roots (or one real root with a multiplicity of two). Graphically, this means that the curve is tangent to the x-axis at the vertex of the parabola and there is one point of intersection, or one x-intercept.
If the discriminant <0, (negative), then there are no real roots, although there is a conjugate pair of complex roots involving the imaginary number i where i is defined as  . Graphically, the curve will have no points of intersection with the x-axis.
|
|
|
